- •I. Тарау. Тау жыныстары ретіндегі грунттардың физикалық қасиеттері
- •1.1. Грунттардың жаратылысы, құрамы
- •1.2. Грунттың қатты түйіршіктері
- •1.3. Грунт құрамындағы судың түрлері мен қасиеттері
- •1.4 Грунт құрамындағы газдар
- •1.5 Грунттардың құрылымы, текстурасы және құрылымдық байланыстары.
- •1.6. Грунттардың физикалық қасиеттерінің сипаттамалады.
- •1.7.Грунттардың жіктелу көрсеткіштері.
- •II тарау. Грунттардың механикалық қасиеттері
- •2.1. Грунт механикасының негізгі заңдылықтар
- •2.2. Грунттардың сығылғыштығы. Нығыздалу заңы.
- •2.3. Грунттардың суөткізгіштігі. Ламинарлық сүзілу заңы
- •2.4. Грунттардың ығысу кедергісі. Кулон заңы
- •2.5 Сызықтық деформациялану принциптері
- •Ι ι ι тарау. Грунттардың кернеулі күйін анықтау
- •3.1. Грунттағы кернеулердің кеңістік есеп жағдайында таралуы
- •3.1.1. Қадалған күштің әсері. Буссинеск есебі
- •3.1.2. Бірнеше қадалған күшретдің әсері.
- •3.1.3. Біркелкі таралған жүктің әсері.
- •3.2. Грунттағы кернеулердің жазық есеп жағдайында таралуы.
- •3.3. Іргетастардың табандары бойынша тірек қысымдарының таралуы.
- •IV тарау. Грунттардың деформацияларын анықтау және іргетастың шөгуін есептеу.
- •4.1 Грунттардың деформацияларының түрлері және маңызы.
- •4.2 Тұтас жүктің әсерінен грунт қабатының шөгуін анықтау.
- •4.2 Есептеу схемасы
- •4.3 Іргетастың шөгуін «грунт қабаттарының деформациясын біртіндеп қосу» әдісімен шешіледі.
- •4.4 Іргетастардың шөгуін «эквивалентті қабат» әдісімен есептеу
- •4.5 Шөгудің уақыт бойынша дамуы. Грунттардың фильтрациялық (сілемдері) консолидациясының теориясы.
- •4.6 Грунттардағы реологиялық құбылыстар
- •Грунттардың шекті кернеулі күйінің теориясы және оның қолдануы.
- •5.1 Жалпы түсініктер
- •5.2 Шамасы үнемі ұлғаятын жүктің әсерінен негізде туындайтын кернеулі күйдің кезеңдері.
- •5.3 Шекті тепе-теңдік күйінің сусыма және иілгіш грунттарға раналған шарттары.
- •5.4.Грунтты негізге түсетін алғашқы қауіпті жүкті анықтау
- •5.5 Грунтты негізге түсетін шекті қауіпті жүкті анықтау
- •5.6 Құламалардың орнықтылығын анықтау
- •5.7 Грунттардың сүйеме қабырғаларға түсіретін қысымын анықтау.
- •5.7.1.Жалпы түсініктер
- •5.7.2.Сусыма грунттың сүиеме қабырғаға түсіретін қысымын анықтау
- •5.7.3. Байланысқан (балшықты) грунттың сүиеме қабырғаға түсіретін қысымын анықтау.
- •Әдебиет
4.4 Іргетастардың шөгуін «эквивалентті қабат» әдісімен есептеу
Сызық дифференцияланатын денелердің теориясының шешімдеріне сәйкес шартты түрде тұтас, изотропты материалдан тұратын жартылай кеңістік ретінде қарастырылатын грунтты негіздің бетінің жергілікті таралған жүктің әсерінен шөгуі Шлейхердің формуласы бойынша анықталады:
![]() (4.8)
(4.8)
Мұнда
![]() - іргетастың қатқылдығы мен табанының
пішінінің ескеретін коэффицент;
- іргетастың қатқылдығы мен табанының
пішінінің ескеретін коэффицент; ![]() - жүк таралған ауданның (іргетастың)
ені;
- жүк таралған ауданның (іргетастың)
ені; ![]() - грунттың Пуассон коэффиценті;
- грунттың Пуассон коэффиценті;![]() - іргетастан грунтты негізде берілетін
қосымша нығыздаушы қысым.
- іргетастан грунтты негізде берілетін
қосымша нығыздаушы қысым.
Егер (2.8) формуласын еске түсірсек:
![]()
Мұнда
![]()
Енді
![]() мен
мәндерін (4.8) формуласына қойсақ:
мен
мәндерін (4.8) формуласына қойсақ:

Сондай – ақ, мынадай белгі енгізсек:
![]() (4.9)
(4.9)
Онда:
![]() (4.10)
(4.10)
Егер (4.4)формуласын еске алсақ:
![]()
Мұнда
![]() бетіне қарқындылығы
бетіне қарқындылығы ![]() - тұтас жүк түсірілген грунт қабаты
екені мәлім.
- тұтас жүк түсірілген грунт қабаты
екені мәлім.
Енді
(4.10) және (4.4)формулаларын салыстыра
отырып, ![]() =Р
нығыздаушы қысымдарын ескерсек, онда
=Р
нығыздаушы қысымдарын ескерсек, онда
![]() көбейтіндісін – тұтас жүктің әсерінен
шөгу шамасы іргетастың шөгуіне тең
эквивалент (балама) қабаттың қалыңдығы
деп қарастыруға болады:
көбейтіндісін – тұтас жүктің әсерінен
шөгу шамасы іргетастың шөгуіне тең
эквивалент (балама) қабаттың қалыңдығы
деп қарастыруға болады:
![]() (4.11)
(4.11)
Сонымен іргетастың шөгуін «эквивалентті қабат» әдісімен есептеуге арналған профессор Н.А.Цытовичтің формуласы мынадай түрге ие болады:
![]() (4.12)
(4.12)
Мұнда
көбейтінді ![]() - эквивалент қабаттың коэффиценттері
деп аталады, ал оның мәндері кестелерде
келтірілген.
- эквивалент қабаттың коэффиценттері
деп аталады, ал оның мәндері кестелерде
келтірілген. ![]() .
.
Түрлі грунт қабаттарынан құралған әртекті негіздің шөгуін есептеу ұшін қажет салыстырмалы сығылу коэффиценттернің орташа мәнін мына формула арқылы есептейді. (4.3 - сурет):
![]()
![]() (4.13)
(4.13)


4.4
– сурет.ғимараттың іргетастарының
уақыт бойынша әркелкі шөгуі: а – күрделі
негіз; ә – іргетастардың уақыт бойынша
шөгуі /
![]() =US
графиктері/
=US
графиктері/
Мұнда
![]() -
негіздің сығылу қалыңдығының:
-
негіздің сығылу қалыңдығының: ![]() ,
бойынша орналасқан грунт қабаттарының
саны
- нөмірі i
грунт қабатының қалыңдығы; салыстырмалы
сығылу коэффиценттері;
,
бойынша орналасқан грунт қабаттарының
саны
- нөмірі i
грунт қабатының қалыңдығы; салыстырмалы
сығылу коэффиценттері; ![]() - нөмірі i
грунт қабатының қалыңдығы; салыстырмалы
сығылу коэффиценттері;
- нөмірі i
грунт қабатының қалыңдығы; салыстырмалы
сығылу коэффиценттері; ![]() - нығыздаушы қысымның (немесе тік
кернеудің
)
эквивалентті үшбұрышты эпюрасының
төменгі ұшы мен нөмірі i
қабаттың
ортасының ара қашықтығы.
- нығыздаушы қысымның (немесе тік
кернеудің
)
эквивалентті үшбұрышты эпюрасының
төменгі ұшы мен нөмірі i
қабаттың
ортасының ара қашықтығы.
4.5 Шөгудің уақыт бойынша дамуы. Грунттардың фильтрациялық (сілемдері) консолидациясының теориясы.
Егер
үйлер мен ғимараттар суға қаныққан
(шалшықты) балшықты грунттарға салынатын
болса, онда олардың іргетастарының
шөгуі көп уақытта, тіпті кейде ондаған
жылдарға созылуы мүмкін. Өйткені мұндай
грунттардың іргетас арқылы түскен
жүктердің әсерінен толық нығыздалуы
үшін олардың кеуектеріндегі судың
сығылып, үзіліп шығуы (фильтрация
консолидациясының дамуы) қажет. Демек
осындай жағдайда салынған ғимараттардың
шөгу жылдамдығы олардың грунтты
негіздерінің су өткізгіштік қабілетіне
байланысты болады. Неғұрлым грунттың
фильтрация коэффиценті ![]() үлкен болса, соғұрлым нығыздалу
деформациясы тез өсіп, өзінің ақырғы
тұрақты шамасына жетеді. Керісінше су
өткізгіштік қабілеті төмен грунттарда
(балшық, мыи балшық) нығыздалу деформациясы
баяу дамиды.
үлкен болса, соғұрлым нығыздалу
деформациясы тез өсіп, өзінің ақырғы
тұрақты шамасына жетеді. Керісінше су
өткізгіштік қабілеті төмен грунттарда
(балшық, мыи балшық) нығыздалу деформациясы
баяу дамиды.
Кейбір
жағдайларда ғимараттардың шөгуінің
уақыт бойынша созылуы олардың негізін
құрайтын грунттардың жылжу деформациясына
(екінші консолидациясына) да байланысты
болуы мүмкін. Дегенмен суға қаныққан
грунттардың созылмалы шөгуінің негізгі
бөлігін олардың кеуектеріндегі судың
сығылып, сүзіліп шығуына тікелей тәуелді
нығыздалу деформациясы құрайды. Сондықтан
инженерлік есептеулерде қарастырылып
отырған мәселені қарапайым түрге дейін
оңайлату үшін грунттардың жылжу
деформациясы ескерілмейді. Іргетастардың
грунтталған негіздерінің нығыздалу
деформациясын уақыт бойынша есептеу
оларды жобалау барысында, құрылыс
нормаларының талаптарына сәйкес,
ғимараттардың шөгуінің әркелкілігін
бағалау үшін қажет. Мысалы: 4.4 – суретте
көрсетілген ғимараттың іргетастарының
(І1 және І2) шөгуі біркелкі болмауы мүмкін.
Өйткені олар су өткізгіштігі бірдей
емес грунттарға орналасқан: ![]() мұнда
мұнда ![]() және
және ![]() құм мен саздақ филбтрация коэффиценттері.
Сондықтан саздаққа салынған іргетасқа
қарағанда
құм мен саздақ филбтрация коэффиценттері.
Сондықтан саздаққа салынған іргетасқа
қарағанда ![]() ,
құмға орналасқан іргетас
,
құмға орналасқан іргетас ![]() тезірек отырады. Мұның өзі грунтты
негіздің әркелкі шөгуін туғызады, жалпы
ғимараттың қаңқасын диформацияға
ұшуратуы мүмкін.
тезірек отырады. Мұның өзі грунтты
негіздің әркелкі шөгуін туғызады, жалпы
ғимараттың қаңқасын диформацияға
ұшуратуы мүмкін.
Ғимараттың суға қаныққан (шылқыған) грунттарға орналасқан іргетастарының уақыт бойынша шөгуін есептеу үшін мынадай баста жорамалдарға негізделген «фильтрациялық (сүзілмелі) консолидация теориясы» қолданылады:
Қалыңдығы h қабат бос, сығылмайтын және гидравликалық үздіксіз суға қаныққан біртекті грунттан тұрады;
Грунт қаңқасы сызық деформацияланатын дене болғандықтан кернеу туындаған сәтте сығылады;
Грунттың құрылымдың беріктігі болмағандықтан, сыртқы жүктің әсерінен туындайтын қысым алғашқы түскен сәтте толығымен кеуек суына беріледі;
Грунт кеуектеріндегі судың қозғалу құбылысы ламинарлық сүзілу заңына бағынады.
Осы жорамалға сәйкес, суға қаныққан қалыңдығы һ грунт қабатының бетіне тұтас біркелкі таралған жүктің Р әсерінен нығыздалуының барысы кеуек суының біртіндеп, жоғары қарай сүзіліп, сыртқа сығылып шығуына тікелей тәуелді болады. (4.5 - сурет). Демек, өзара байланысты екі құбылыс қатарынан жарылып, жүріп отырады. Осы құбылыстарды, атап айтқанда, грунт кеуегінен судың сыртқа сығылып шығуын – ламинарлық сүзілу заңымен, ал грунттың нығыздалуын, кеуектілік коэффицентттерінің өзгеруімен байланыстырып, - нығыздалу заңымен анықтауға болады екен.
Су сүзіліп шығатын гркнт қабатының (4.5 - сурет) бетінің z тереңдіктегі нүкте үшін кез келген уақыт сәтінде (2.12) формулаға сәйкес мынадай шарт орындалады:
![]() (4.14)
(4.14)
Мұнда
- суға қаныққан грунт қабатының бетіне
таралған қысым; ![]() - грунттың қаңқасына (қатты түйіршіктеріне)
берілетін «тиімді» қысым;
- грунттың қаңқасына (қатты түйіршіктеріне)
берілетін «тиімді» қысым; ![]() - кеуек суының берілетін «бейтарап»қысым.
«Тиімді» қысым грунттың нығыздалуын
мүмкін ететін болса, «бейтарап» қысым
кеуек суында арын тудырып, судың сыртқа
сығылып, сүзіліп шығуын, яғни қозғалуын
мәжбүр етеді.
- кеуек суының берілетін «бейтарап»қысым.
«Тиімді» қысым грунттың нығыздалуын
мүмкін ететін болса, «бейтарап» қысым
кеуек суында арын тудырып, судың сыртқа
сығылып, сүзіліп шығуын, яғни қозғалуын
мәжбүр етеді.
Грунт қабатыныңбетіне сыртқы жүкті түсірген алғашқы сәтте (4.14) шартына сәйкес қысым толығымен кеуек суымен қабылданады.

4.5 – сурет. Суға қаныққан грунт қабатының уақыт бойынша шетуін есептеуге арналған схема:
І – судың сүзілу бағыты.

4.6 – сурет. Нығыздаушы қысымның таралу түрлері:
А – жағдай «0»; ә – жағдай «І»; б – жаңдай «2»
![]()
Мұның әрі қарай, уақыт өткен сайын, (4.14) шарты бойынша «бейтарап» қысымның үлесті мөлшері көбейіп, осыған байланысты грунт қабатының нығыздалу процесі қарқындай түседі:
![]() ,
,
Егер уақыт ұзаққа созылса:
![]()
Енді
жоғарыда айтылған екі құбылыстың
(нығыздалу және сүзілу) даму заңдылықтарын
қарастырайық. Ол үшін грунт қабатының
(4.5 - сурет) бетінен z тереңдікте орналасқан
қалыңдығы dz грунт қабатшасының көлеміндегі
сүзіліп сыртқа шығатын судың шығыны
![]() , сол көлемнің ішіндегі кеуектіліктің
, сол көлемнің ішіндегі кеуектіліктің
![]() уақыт аралығында азаюына тең болады
деп жорамал қабылдаймыз, демек:
уақыт аралығында азаюына тең болады
деп жорамал қабылдаймыз, демек:
![]() (4.15)
(4.15)
Бұл теңдеудің сол жақ бөлігінің ламинарлық сүзілу заңын қолдансақ:
![]() (4.16)
(4.16)
онда:
![]() (4.17)
(4.17)
Мұнда
![]() - кеуек суында туындайтын арын екенін
және
- кеуек суында туындайтын арын екенін
және
Мыналарды
ескерсек: ![]() ;
;
Сонда:
![]() (4.18)
(4.18)
Сөйтіп, (4.15 ) теңдеуінің сол жақ бөлігі мынадай түрге ие болады:
![]() ;
(4.19)
;
(4.19)
Енді
(4.15) теңдеуінің оң жақ бөлігіне нығыздалу
заңын қолдансақ және грунт кеуектілігінің
формуласының: ![]() бөлігіндегі е мәнін 1 – мен салыстырғанда
өзгермейтін
бөлігіндегі е мәнін 1 – мен салыстырғанда
өзгермейтін ![]() орташа тұрақты шама деп, жорамалдап
қабылдасақ:
орташа тұрақты шама деп, жорамалдап
қабылдасақ:
 4.20
4.20
Нығыздалу заңын ескерсек (2.6):
 бұл
мәнді (4.20) формуласына қойсақ:
бұл
мәнді (4.20) формуласына қойсақ:
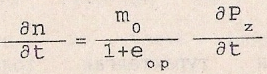
Мұнда
![]() екенін ескерсек және (4.15) теңдеуінің
екі жақ бөліктерінің қорытынды мәндерін
қойып, тұрақты шамаларды сол жаққа
шығарсақ:
екенін ескерсек және (4.15) теңдеуінің
екі жақ бөліктерінің қорытынды мәндерін
қойып, тұрақты шамаларды сол жаққа
шығарсақ:
 4.21
4.21
Осы теңдеудің сол жағындағы шамасы тұрақты көбейткішті былай белгілесек:
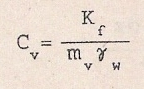 4.22
4.22
Мұнда Cv – грунттың консалидация коэффициенті. Сонда (4.21) теңдеуі біржолата мынадай түрге ие болады:
 4.23
4.23
Бұл формула грунттардың сүзілмелі (фильтрациялық) консалидациясының теориясының бір өлшемді есебінің дифференциалдық теңдеу болып табылады. Осы теңдеудің шешімін алғашқа шекараалық шарттарды қанағаттандыратындай жағдайда Фурье қатарын қолдану арқылы шығарады. Егер тас үстінде жатқан (4.5 сурет) қалыңдығы z=h суға қаныққан грунт қабатының таралған тұтас жүктің Р әсерінен нығыздалу барысында сығылып шығатын кеуек суы тек қана бір бағытта (тік жоғары қарай) сүзіліп жылжитын болса, онла Фурье қатарынан бірінші мүшесін шектеліп, (4.23) теңдеуінің шешімін мынадай қарапайым түрге келтіруге болады [4]:
![]() 4.24
4.24
Мұнда е- натуралды логарифмдер негізі;
 4.25
4.25
бұл формуладағы t- грунт нығыздалу уақыты.
Құрылыс ісі үшін іргетастың шөгуінің уақыт бойынша өсуін анықтаудың маңызы зор:
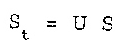 4.26
4.26
Мұнда S – іргетастың шөгуінің тұрақталған толық шамасы, U- грунт қабатының нығыздалу дәрежесі (консолидация дәрежесі) бұл параметрдің мендері 0 мен 1 аралығында өзгереді. Мысалы, грунттың ңығыздалуы аяқталған сәтте U=1, ал оның нығыздалуы барысында: 0<U<1 (4.26) формуласынан нығыздалу дәрежесін былай анықтауға болады:
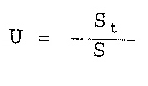 4.27
4.27
Бұл теңдеудіматематикалық түрде былай жазуға болады (4.5-сурет):
 4.28
4.28
Мұнда бөлшектің бөлімінде шөгудің тұрақталған толық шамасына сәйкес келетін нығыздаушы (тиімді) қысымның эпюрасының ауданы көрсетілген, ал бөлшектің алымында шөгудің тұрақталмаған шамасына сәйкес келетін нығыздайшы (тиімді) қысымның эпюрасының ауданы келтірілген. Енді осы формулаға Pz (t) (Фурье қатары түріндегі ) (4.24) мәнін қойып, интегралды шешсе:
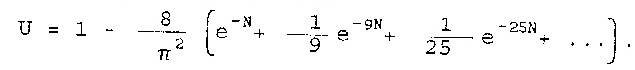 4.29
4.29
Консолидация
дәрежесінің осы мәні бір өлшемді есеп
үшін нығыздаушы қысымның шамасы грунт
қабатының бойында тұрақты болғанда
Pz=P=const,
яғни оның эпюрасы P![]() H
төрт бұрышымен анықталатын жағдайға
арналып шығарылған(4.6-сурет, 0 жағдай).
Сығылатын грунт қабатының бойында әсер
ететін нығыздаушы қысымның құрылыс
ісінде қолданылуы мүмкін таралу
заңдылықтары 4.6-суретте көрсетілген.
Жағдай «1» грунт салмағының әсерінен
туындайтын нығыздаушы қысымның (тік
кернеудің ) эпюрасын бейнелейді. Жағдай
«2 » жергілікті (іргетастың табаны
бойынша) таралған күштің әсерінен
туындайтын нығыздаушы қысымның (тік
кернеудің) эпюрасын жуықтап көрсетеді,
мысалы проф.Н.А.Цытовичтің «эквивалент
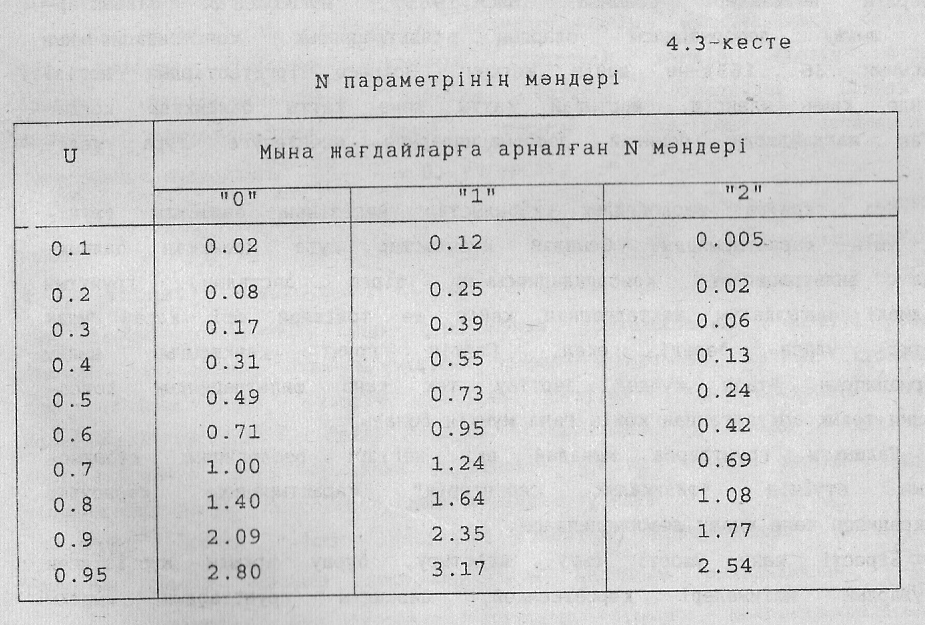
қабат» әдісіне сәйкес. 4.3- кестеде «0»,
«1» және «2» жағдайларына арналған N
параметрлерінің мәндері келтірілген.
H
төрт бұрышымен анықталатын жағдайға
арналып шығарылған(4.6-сурет, 0 жағдай).
Сығылатын грунт қабатының бойында әсер
ететін нығыздаушы қысымның құрылыс
ісінде қолданылуы мүмкін таралу
заңдылықтары 4.6-суретте көрсетілген.
Жағдай «1» грунт салмағының әсерінен
туындайтын нығыздаушы қысымның (тік
кернеудің ) эпюрасын бейнелейді. Жағдай
«2 » жергілікті (іргетастың табаны
бойынша) таралған күштің әсерінен
туындайтын нығыздаушы қысымның (тік
кернеудің) эпюрасын жуықтап көрсетеді,
мысалы проф.Н.А.Цытовичтің «эквивалент
қабат» әдісіне сәйкес. 4.3- кестеде «0»,
«1» және «2» жағдайларына арналған N
параметрлерінің мәндері келтірілген.
Сөйтіп қарастырылған формулалар мен кестені пайдаланып сулы грунттарға салынған іргетастардың шөгу жылдамдығын бағалауға болады. Ол үшін шөгудің уақыт бойынша дамуын зерттеп, оның графиктерін салады. Әуелі 4.3- кестеде келтірілген U параметрінің 0 мен1 аралығындағы мәндерін (U1) қабылдайды. Сонан кейін осы мәндерге сәйкес келетін грунттың шөгу шамаларын (Sti) (4.26) формула бойынша есептеп, ал уақыт мәндерін (ti) мына формула арқылы табады:
 4.30
4.30
Мұнда Ni мәндерін 4.3-кесте бойынша Ui мәндеріне және нығыздаушы қысымның эпюрасының пішініне (4.6-сурет) байланыс қабылдайды.
Осылайша
Sti=Ui
![]() тәуелділігінің
графигін салуға болады.(4.4, ә –)
тәуелділігінің
графигін салуға болады.(4.4, ә –)