3.2. Грунттағы кернеулердің жазық есеп жағдайында таралуы.

Күш таралған төртбұрышты ауданның ұзындығынан 1және b қатынасының шамасы үлкейген сайын грунтты негізде туындайтын кернеулі (ленталы) іргетас үшін 1: b 10 болса, онда ол өзінің грунтты негізімен бірге «жазық есеп» жағдайында жұмыс атқарады деп саналады. Осындай грунтты негіздің кез келген нүктесінің «жазық есепке» сәйкес деформациялық күйі мыныдай «жазық деформация» шартымен анықталады:

; , яғни деформация тек қана YOZ жазықтығында дамиды (3.7 - сурет).

Фламан Буссинесктің кеңістікке арналған есебін жартылай жазықтық үшін қарастырып, сызықтық жүктің (Т/М әсерінен «жазық есеп» жағдайында грунтта туындайтын кернеулерді есептеуге арналған теңдеулерді шығарды (1.4.).

Кейінне Митчелл (1900) және тағы басқалар Фламанның есебін пайдаланып, ондағы сызықтық жүктің орнына жолақ аудан бойынша таралған жүкті элементар жүктердің (p dy 1м) қосындысы ретінде қарастырып, «жазық есеп» жағдайында грунтта туындайтын кернеулерді есептеуге арналған формулалар шығарды. Осындай есептердің құрылыс тәжірибесінде кеңінен қолданылған шешімдеріне тоқталайық.

Изотропты сызық деформацияланатын жартылай кеңістіктің бетіне жолақ аудан арқылы таралған жүктің әсерінен сол кеңістіктің кез келген нүктесінде туындайтын кернеулік күй мынадай құрамдас кернеулермен анықталады және (3.7- сурет),

( )

(3.15)

мұнда «көрініс бұрышы», ( ).

Бұл формулалар «ықпал коэффициенттерін» енгізу арқылы мынадай қарапайым түрге келтірілген:

= (3.16)

= (3.16a)

= (3.16ә)

мұнда «ықпал коэффициенттері», мәндері кернеулік күйі анықталатын нүктенің салыстырмалы координаттарына (z/b және y/b ) байланыстты кесте бойынша (Н.А.Цытович , 1983) анықталады. Осы формулалар арқылы жолақ іргетастың грунтты негізінің тік және көлденең қималарында сығу кернеулерінің ( ) таралу ерекшеліктерін көрсететін эпюралар тұрғызуға болады. (3.8 - сурет)

Мұндай эпюралар бойынша «бірдей кернеулер сызықтарын» көрсетуге болады. (3.9 - сурет). Осындай сызықтар грунтты негіздің кернеулік күйін бағалап, кернеулер неғұрлым шоғырланған, яғни іргетастың орнықтылығына қауіп туғызуы мүмкін аймақтарға ерекше назар аударуға мүмкіндік береді. Мысалы; тік сығу кернеулерінің «бірдей кернеулер сызықтары» (изобаралар) іргетастың астындағы грунтты оның нығыздалу дәрежесі бойынша бөлек аймақтарға бөліп қарастыруға мүмкіндік береді. Сондай ақ жанама кернеулердің «бірдей кернеулер сызықтары» іргетасқа берілетін жүкті өсіргенде негізде бірінші кезекте ең қауіпті ығысу деформациялары туындайтын аймақтар сол іргетастың бұрыштарында болатынын көрсетті.

Іргетастар мен негіздерді жобалау барысында кей жағдайларда басты кернеулерді , анықтау қажет болады. Мұндай кернеулердің жанама кернеулері нольге тең басты алаңшаларда әсер ететіні белгілі. Митчеллдің шешуі бойынша басты кернеулер мына формулалар арқылы анықталынады (3.10 - сурет):

):

): )

мұнда «көрініс бұрышы» өлшемі радиан). Үлкен басты кернеу көрініс бұрышының биссектрисасы бойынша бағытталған.

3.8 – сурет. Грунтты негіздің тік /а/ және көлденең /ә/ қимасындағы сығу кернеулерінің эпюралары.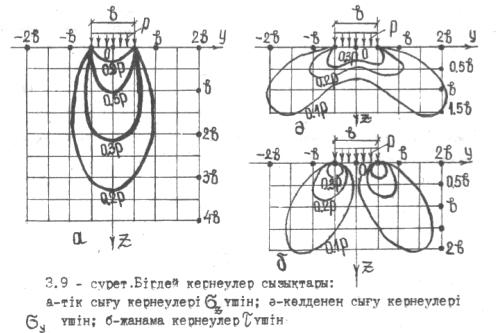

3.9 – сурет. Бірдей кернеулер сызықтары:

а – тік сығу кернеулері үшін; ә – көлденең сығу кернеулері үшін; б – жанама кернеулер үшін.

3.10 – сурет. Басты кернеулер эллипстері.