Ι ι ι тарау. Грунттардың кернеулі күйін анықтау
Кәдімгі денелер (болат, бетон, тас, грунт) сыртқы күштің әсерінен өздерінің өлшемдері мен пішіндерін өзгертеді, яғни деформацияланады. Осындай жағдайда дененің бөлшектерінің арасында ішкі қарсы әсер етуші кернеулердің жиынтығын айтады.
Құрылыс ісінде қолданылатын грунттардың кернеулі күйін грунт механикасы "сызық деформацияланатын денелер теориясымен" толықтырылған "серпімділік теориясының" формулалары арқылы анықтауды ұсынады. 2 тарауда айтылғандай (2.5), бұл теорияның басты жорамалына сәйкес шартты түрде грунт – тұтас, жалпы деформациялар модулімен сипатталатын сызық деформацияланатын дене ретінде қарастырылады.
Грунттардың кернеулі күйін есептеудің құрылыс үшін мынадай үлкен тәжірибелік маңызы бар:
Іргетастардың табандарының өлшемдерін есептеу үшін.
Ғимараттардың грунтты негіздерінің сығылуын (шөгуін) анықтау үшін.
Ғимараттардың грунтты негіздерінің, құламалардың, сүйеме қабырғалардың беріктілігін (орнықтылығын) есептеп бағалау үшін.
3.1. Грунттағы кернеулердің кеңістік есеп жағдайында таралуы
3.1.1. Қадалған күштің әсері. Буссинеск есебі
Сызық
деформацияланатын жартылай кеңістіктің
бетін шектейтін көлденең жазықтықтың
Ο нүктесіне тік қадалған күштің Ρ әсерін
қарастырайық (3.1,3.2 - суреттер). Осындай
жағдайда жартылай кеңістіктің кез
келген нүктесінде туындайтын
кернеул-деформациялы күйді мынадай
алты құрамдас кернеулермен
,
,
, 
,
,
және
үш құрамдас деформациялармен (орын
ауыстырулармен)
,
, 
анықтауға болады. Бұл есепті 1885ж.
Профессор Буссинеск шешкен.
Есепті
шешудің барысында R және β полярлық
координаталарымен көрсетілген M нүктесіне
қатысты R бағытында әсер ететін 
радиалды кернеуін (3.3 - сурет) табады
және ауыстыру формулалары бойынша M
нүктесі арқылы беткі көлденең жазықтыққа
қатар жүргізілген
3.1
–сурет.
Есептің негізгі схемасы. 3.2- сурет. Беткі
көлденең жазықтыққа қатар орналасқан
жазықшалардағы кернеулерді анықтау
схемасы.
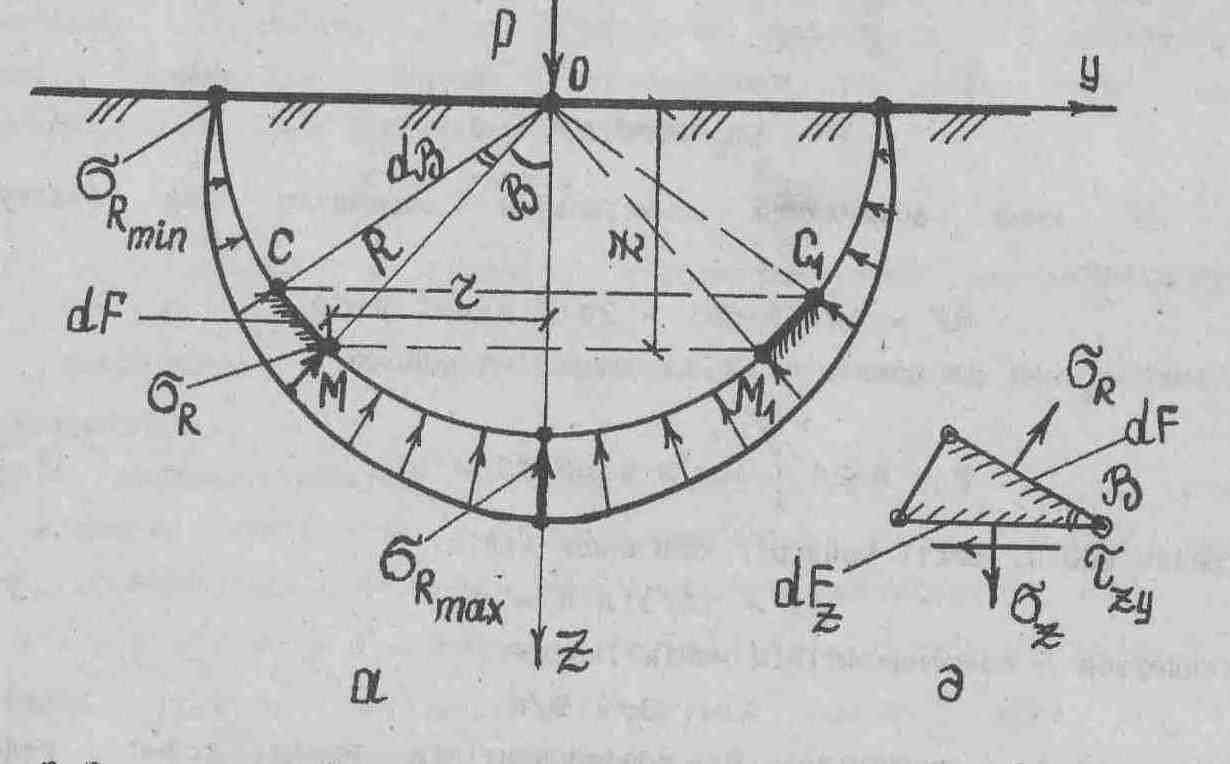
3.3- сурет. Қадалған күштің әсерінен туындайтын радиалдық кернеулер: а- жалпы схема; ә- М нүктесінде әсер ететін кернеулер.
Буссинеск есебінің шешімін қарапайым түрде қарастыру үшін 3.3- суретке мынадай постулат қабылдаймыз:
(3.1)
мұнда
-
тепе теңдік шарты бойынша анықталынатын
коэффициент.
Енді
тепе теңдік шартын анықтау үшін центрі
күш Ρ
қадалған О нүктесі болатындай жарты
шар түріндегі қиманы қарастырамыз
(3.3- сурет) ( 3.1 ) формуласына сәйкес
-
дің шамасы 
(беткі көлденең жазықтықта, яғни 
болғанда ) және 
( OZ ось бойынша Z = R тереңдікте, яғни
болғанда ) аралығында өзгереді. Алайда
центрлік бұрышы 
ға тең элементар шар белдеуі ( Мс 
) үшін 
деп қабылданады.
Тепе теңдік шарты бойынша барлық күштердің тік бағыттағы оське ( OZ )
түсірілген проекцияларының қосындысы нольге тең болу керек:
P
- 
(3.2)
мұнда
мына формуламен анықталатын элементар
шар белдеуінің бетінің ауданы:
Енді
мен
мәндерін 
теңдеуіне қойсақ:
P
- A
(3.3)
Интегралды шешіп, шекті мәндерді қойғаннан кейін:
P
-
(
A
(3.4)
Осы теңдеуден А коэффициенттерінің мәнін табамыз:
P
- (
(3.5)
Бастапқы (3.1) теңдеуіне А коэффициенттерінің мәнін қойып, радиалды кернеуді анықтаймыз:
(3.6)
Бұл
кернеу көлбеу алаңша 
тік түседі. Элементар үшбұрышты призманың
(3.3 ә сурет) тепе теңдік күйінің талабына
сәйкес барлық күштердің тік бағыттағы
оське 
түсірілген проекцияларының қосындысын
нольге теңеп жазамыз:
Немесе
Енді
осы теңдеуге
мәнін (3.6) формуласынан қойып, тік кернеуді
табамыз:
Егер
(3.3
- сурет)
екнін ескерсек:
)
Сондай
ақ 
= 
болғандықтан,
қорыта келіп мынадай формуланы қабылдаймыз
k
(3.7)
мұнда:
k
Осындай
жолмен қалған бес құрамдас кернеулер
(
)
мен үш құрамдас деформациялар (орын
ауытқулар) 
да анықталады. Мысалы, беткі көлденең
жазықтықта (О нүктесінің деңгейінде)
орналасқан барлық нүктелердің тік
бағыттағы орын ауыстырулары (шөгуі)
мына формуламен есептелінеді:
(3.8)
Мұнда
- «сызық деформацияланатын жартылай
кеңістіктің коэффиценттері» (
жалпы
деформациялар модулі, 
грунттың
Пуассон коэффиценті).
Сызық деформацияланатын жартыалй кеңістіктің кез – келген нүктесінде қадалған күштің Р әсерінен туындайтын жалпы (толық) кернеу, яғни тік кернеулердің қосындысы мына теңдеулермен анықталады:
=
= (P/
)
(3.9)
Іргетастардың грунтты негіздерінің шөгуін есептеу үшін (3.7) (3.8) және (3.9) формулаларының тәжірибелік маңызы зор.