3)Устройства ввода/вывода

На рис. 2.19, б показан пример организации дешифрации адреса внешних устройств. Схема позволяет подключать к магистралям до 64 устройств ввода/вывода. Использование четырех таких схем реализует возможности в микропроцессорной БИС по адресации внешних устройств. Дешифратор адреса Д2, стробируемый сигналом чтения ввода (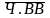 ) или записи ввода/ вывода 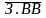для выбора либо дешифраторов адреса для восьми простейших регистров ввода, либо схем, содержащих несколько таких регистров (КР580ВВ55, КР580ВВ51, КР580ВТ57, КР580ВИ53, КР580ВН59). В качестве простейшего устройства на рис. 2.19, б показан регистр ввода/вывода К589АП16. Входные сигналы подключаются ко входам А0-А3 микросхем Д4, Д5, а выходные к выходам С0-С3.

При обращении к устройствам ввода/вывода и к ячейкам памяти дешифраторы адреса должны стробироваться сигналами 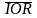, , , . При таком способе дешифрации необходимо следить, чтобы адресное пространство устройств ввода/вывода не перекрывалось с адресным пространством микросхем ОЗУ и ПЗУ.

Адресация устройств ввода/вывода производится как старшим байтом магистрали адреса, так и младшим байтом. Оба восьмиразрядных адреса дублируется на соответствующих байтах шины адреса.

7. Разобрать фрагмент программы с использованием асинхронно-программного обмена информацией. Тип микропроцессора определяет студент. Дать структурную схему.

-

8. Методы преобразования десятичных чисел в двоичный, восьмеричный и шестнадцатеричный код.

1. Целая часть

Повторное деление данного десятичного числа на основание, остатки дают преобразованное число, читаемое в направлении снизу вверх.

1) 10^-ое  2^-ое ост.

3 62=18 0

182=9 0

92=4 1 36₁₀=100100₂

4:2=2 0

2:2=1 0

1:2= 1

ост.

124:2=62 0

62:2=31 0

32:2=15 1 124₁₀=1111100₂

15:2=7 1

7:2=3 1

3:2=1 1

1:2= 1

2) 10^ое 8^ое ост.

36:8=4 4

4:8= 4 36₁₀=44₈

3) 10^ое 16^ое ост.

36:16=2 4

2:16= 2 36₁₀=24 H

ост.

124:16=7 C

7:16= 7 124₁₀=7C H

2. Преобразование дробных десятичных чисел в двоичные, восьмеричные, шестнадцатеричные коды

Повторное умножение данного десятичного числа на основание. Разряд перед запятой дает разряд преобразованного числа, при последующем умножении используется лишь дробная часть промежуточного результата.

1. 0,375 D B (двоичная система)

0 ,3752=0,75 0

0,752=1,5 1 0,375 D=0,011₂

1,52=1,0 1

2) 0,375 DQ

0,3758=3,0 3 0,375 D=0,3₈=0,3Q

3)0,375 DH

0,37516=6,0 6 0,375 D=0,6 H

9. Методы преобразования двоичных, восьмеричных и шестнадцатеричных чисел в десятичные.

1. Целая часть

Повторное умножение промежуточного результата на основание и сложение его со значением разряда данного числа. Первым промежуточным результатом является наивысший разряд.

1) 110100₂  D

1 1

12+1 3

32+0 6

62+1 13

132+0 26

262+0 52

32 16 8 4 2 1

1 1 0 1 0 0 110100₂ = 52 D

2 ) 154 Q D

1 1

18+5 13

138+4 108

1 5 4 Q=108 D

3) 1AF H D

1 1

116+A 26

2616+F 431

1 A F H=431 D

2. Перевод дробных кодов в десятичные

Повторное деление суммы промежуточного результата и значения разряда данного числа на основание. Первым промежуточным результатом является младший разряд, делённый на основание.

1) 0D

1:2=0,5

+0,5:2=0,75

+0,75:2=0,875

0, 1 1 1 0,111₂=0,875D

2) QD

1:8=0,125

+0,125:8=0,64

+0,64:8=0,455

0, 3 5 1 0,351₈=0,455D

3) HD

A:16=0,625

+0,625:16=0,101

0, 1 A 0,1A₁₆=0,101D

Общее правило

В общем случае перевод целого числа из одной системы счисления в другую производится методом повторного деления данного числа на основание той системы, в которую оно переводится. Деление выполняют в системе счисления, в которой записано подлежащее преобразованию число. Основание записывают в системе счисления преобразуемого числа. Результат также записывают в системе преобразуемого числа.

1. 154QD

154. 12

1 2 12 12

34 12 1 12

24 0 1 0

10

8 0 1 154₈ = 108₁₀

2. 10000₂D

1 0000 1010

1010 1 1010

110 1

10000₂ =16₁₀

По общему правилу перевод дробной части числа из одной системы счисления в другую производится последовательным умножением числа на основание преобразованного числа. Умножение производится в системе счисления преобразуемого числа, основание и результат записываются в системе счисления преобразуемого числа. Умножению подвергаются только дробные части промежуточных результатов. Целая часть до запятой представляет собой разряды преобразуемого числа, записанные в системе счисления преобразуемого числа.

0,752QD

0,752  12

11 444

5 550

7 02

1)  0,752

12

1724

752

11,444

2)  0,444

12

1110

444

5,550

3)  0,55

12

132

55

7,02

0,752 Q = 0,957 D