Основна макроекономічна тотожність

Сукупна пропозиція визначається за допомогою наведеної вище виробничої функції Р. Солоу:

y = f(k),

де у — випуск продукції на одиницю праці, а k — обсяг капіталу на одиницю праці.

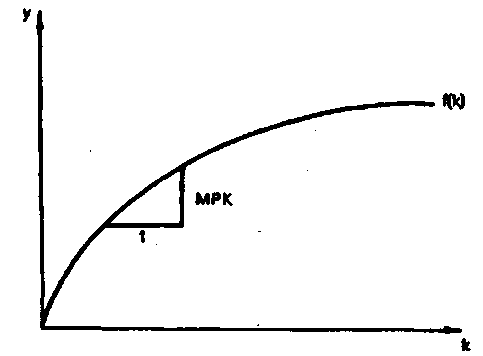
Рис. 1. Графік виробничої функції Р. Солоу

Виробнича функція ілюструє, як накопичення капіталу на одного зайнятого (капіталомісткість праці) впливає на продуктивність праці (випуск на одного зайнятого). Чим більший обсяг такого капіталу, тим з часом меншою стає його віддача у вигляді граничної продуктивності додаткової одиниці капіталу (МРК).

Рис. 1 ілюструє спадаючу граничну продуктивність капіталу. Це означає, що кожна додаткова одиниця капіталу забезпечує менше зростання випуску на зайнятого робітника, ніж попередня додаткова така одиниця. Це зростання випуску позначає темпи економічного зростання (МРК), який фіксується для кожного значення запасу капіталомісткості праці на горизонтальній осі (k):

МРК = f(k+1) – F(k),

де МРК — гранична продуктивність капіталу.

Накопичений капіталу, таким чином, має сенс не завжди.

Настає момент у цьому процесі, коли, додатковий капітал не сприяє збільшенню випуску продукції.

Сукупний попит у моделі Солоу задається через споживання та інвестування на одиницю праці.

y=c+i при

де с — споживання, а і — інвестування на одиницю праці.

Точки врівноваження економічної системи задаються умовою рівності інвестицій та обсягів заощадження. Тому компонент інвестицій для станів рівноваги можна виразити за допомогою величини заощаджень, користуючись нормою заощадження (s) у сукупному доході суспільства:

i = sy => i = sf(k)

Виразивши, таким чином, основні компоненти макроекономічної тотожності на одиницю праці, ми отримали їхні функції від одного незалежного змінника — k: у = с + і при

с = f(k), с = (1-s)f(k), і = sf(k).

Тепер можна ці функції кінцевого продукту, споживання та інвестицій зобразити графічно на моделі Р. Солоу "продуктивність — капіталомісткість" (див. рис. 2).

Рис. 2 Основне макроекономічне рівняння в моделі Солоу

Компоненти тотожності "доход-витрати", які ми позначали як у = с + i, на графіку репрезентовано відрізками: у = ak; с = ab; і = bk. Тут ми бачимо, що норма заощадження s зумовлює розподіл кінцевого продукту (доходу) на одиницю праці на споживання та заощадження. І все це подано як функції від змінника k, тобто обсяги доходу, споживання та заощадження функціонально залежать від обсягу накопиченого запасу капіталу (на одиницю праці).

Визначення сталої врівноваженості

Принциповим питанням визначення перспективи економічного зростання є відшукання точки сталої врівноваженості економічної системи, для чого насамперед необхідно проаналізувати процес накопичення запасу капіталу країни. Цей процес має два протилежних вектори: річні інвестиції та амортизація діючого капіталу. Інвестиції збільшують наявний запас капіталу, а амортизація зменшує його на величину фізичного чи морального зношення та знецінення. Таким чином, зміна запасу капіталу за рік буде визначатися формулою:

k = і —  k,

де k та і — капітал та інвестиції на одиницю праці; — норма амортизації, яка в моделі Солоу є константою.

Станові сталої рівноваги в даній економічній системі буде відповідати такий обсяг k, коли інвестиції зрівняються з амортизацією. Це можна пояснити, якщо розглянути характер економічної динаміки ліворуч та праворуч від цієї точки. При позитивному k, тобто коли інвестиції перевищують амортизацію, запас капіталу в суспільстві збільшиться на цю величину, що згідно з функцією у = f(k) викличе підвищення продуктивності праці (у). При від'ємному k відповідно у понизиться. Таким чином, тільки в точці, де інвестиції дорівнюють амортизації, економічна система (ії випуск у*) набуде сталого врівноваженого стану. Цей процес також можна відобразити графічно (див. рис. 3). Позначимо точку сталої рівноваги k*, де маємо запас капіталу, при якому утворюється довгострокова стала рівновага економіки. Цей обсяг капіталу ще називається постійним рівнем капіталу. Тобто це такий обсяг капіталу на одиницю праці, коли інвестиції зрівняються з амортизацією наявного капіталу, і, відповідно, запас капіталу країни не зростатиме й не буде зменшуватись.

На графіку зображені функція інвестицій і = sf(k) та функція амортизації  k, де  — постійна норма амортизації. Обидві функції мають один аргумент — k. На рисунку видно, що існує один рівень запасу капіталу, за якого інвестиції порівнюють амортизації (k*) і доход суспільства при цьому не змінюється, тобто це — стан сталої рівноваги. Якщо, наприклад, економіка знаходиться в точці k₁, то матимемо позитивний приріст капіталу k = sf(k) -  k. Він додається до обсягу k₁, і згідно з функцією у = f(k) одержимо більший доход на душу населення. Цей процес буде продовжуватися до точки k*, де приріст доходу зупиниться. Якщо економіка перебуватиме у точці k₂, то будемо мати від'ємний д£ і запас капіталу та відповідний доход будуть знижуватися поки процес не вийде на точку k*.