
- •1. Группоид
- •Типы магм
- •2. Полугруппа
- •Примеры
- •4. Кольцо Определение
- •Простейшие свойства
- •Примеры
- •5. Радикал кольца
- •6. Поле
- •7. Алгебра
- •Свойства
- •8. Кольцо многочленов от нескольких переменных Определение
- •9. Симметрический многочлен
- •10. Порядок элемента группы
- •11. Порядок группы
- •12. Смежный класс
- •13. Симметрическая группа
- •Свойства
- •Представление симметрической группы в виде матричной
- •14. Знакопеременная группа
- •15. Циклическая группа
- •16. Факторгруппа
- •17. Нормальная подгруппа
- •18. Центр группы
- •19. Централизатор элемента группы
- •20. Силовская p-подгруппа
- •Необходимые определения
- •Теоремы
- •Следствие
- •21. Сопряжённый элемент группы
- •22. Идеал кольца
- •23. Главный идеал кольца
- •24. Кольцо главных идеалов
- •25. Сумма идеалов
- •26. Факторкольцо
- •27. Характеристика поля
- •28. Представление Определения и концепции
- •Определение
- •29. Модуль
- •30. Примитивный элемент
- •31. Тело
- •32. Алгебраическая система
- •Основные классы алгебраических систем
- •Группоиды, полугруппы, группы
- •Алгебры
- •33. Многообразие
- •35. Дистрибутивная решётка
- •36. Булева алгебра
- •37. Фильтр
- •Определение в рамках теории решёток
- •Фильтры на множествах
- •База фильтра
- •Сравнение фильтров
- •Фильтры в топологических пространствах
- •Примеры
- •38. Ультрафильтр
- •39. Ультрапроизведение
16. Факторгруппа
Факторгруппа — конструкция, дающая новую группу (факторгруппу) по группе и её нормальной подгруппе.
Факторгруппа группы
по
нормальной подгруппе
![]() обычно
обозначается
обычно
обозначается
![]() .
.
Определение
Пусть — группа, и — её нормальная подгруппа. Тогда на классах смежности в
![]()
можно ввести умножение:
![]()
Легко проверить что это умножение не
зависит от выбора элементов в классах
смежности, то есть если
![]() и
и
![]() ,
то
,
то
![]() .
Это умножение определяет структуру
группы на множестве классов
смежности, а полученная группа
называется
факторгруппой
по
.
.
Это умножение определяет структуру
группы на множестве классов
смежности, а полученная группа
называется
факторгруппой
по
.
Свойства
Гомоморфный образ группы До победы коммунизма Изоморфен факторгруппе По ядру гомоморфизма. |
Теорема о гомоморфизме: Для любого гомоморфизма
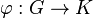
![]() ,
,
то есть факторгруппа
по
ядру
![]() изоморфна
её образу
изоморфна
её образу
![]() в
в
![]() .
.
Отображение
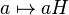 задаёт
естественный гомоморфизм
задаёт
естественный гомоморфизм
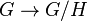 .
.Порядок равен индексу подгруппы
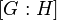 .
В случае конечной группы
он
равен
.
В случае конечной группы
он
равен
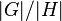 .
.Если абелева, нильпотентна, разрешима, циклическая или конечнопорождённая, то и будет обладать тем же свойством.
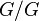 изоморфна
тривиальной группе (
изоморфна
тривиальной группе ( ),
),
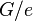 изоморфна
.
изоморфна
.
Примеры
Пусть
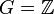 ,
,
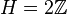 ,
тогда
изоморфна
,
тогда
изоморфна
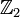 .
.
Пусть
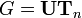 (группа
невырожденных верхнетреугольных
матриц),
(группа
невырожденных верхнетреугольных
матриц),
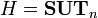 (группа
верхних унитреугольных
матриц), тогда
изоморфна
группе диагональных матриц.
(группа
верхних унитреугольных
матриц), тогда
изоморфна
группе диагональных матриц.
17. Нормальная подгруппа
Норма́льная подгру́ппа (также инвариа́нтная подгру́ппа) — подгруппа особого типа, левый и правый смежные классы по которой совпадают. Такие группы важны, поскольку позволяют строить факторгруппу.
Определения
Подгруппа
![]() группы
называется
нормальной, если она инвариантна
относительно сопряжений, то есть для
любого элемента
из
и
любого
группы
называется
нормальной, если она инвариантна
относительно сопряжений, то есть для
любого элемента
из
и
любого
![]() из
,
элемент
из
,
элемент
![]() лежит
в
:
лежит
в
:
![]()
![]()
Следующие условия нормальности подгруппы эквивалентны:
Для любого из ,
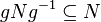 .
.Для любого из ,
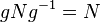 .
.Множества левых и правых смежных классов в совпадают.
Для любого из ,
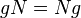 .
.изоморфна объединению классов сопряженных элементов.
Условие (1) логически слабее, чем (2), а условие (3) логически слабее, чем (4). Поэтому условия (1) и (3) часто используются при доказательстве нормальности подгруппы, а условия (2) и (4) используются для доказательства следствий нормальности.
Примеры
и — всегда нормальные подгруппы . Они называются тривиальными. Если других нормальных подгрупп нет, то группа называется простой.
Центр группы — нормальная подгруппа.
Коммутант группы — нормальная подгруппа.
Любая характеристическая подгруппа нормальна, так как сопряжение — это всегда автоморфизм.
Все подгруппы абелевой группы нормальны, так как . Неабелева группа, у которой любая подгруппа нормальна, называется гамильтоновой.
Группа параллельных переносов в пространстве любой размерности — нормальная подгруппа евклидовой группы; например, в трёхмерном пространстве поворот, сдвиг и поворот в обратную сторону приводит к простому сдвигу.
В группе кубика Рубика подгруппа, состоящая из операций, действующих только на угловые элементы, нормальна, так как никакое сопряжённое преобразование не заставит такую операцию действовать на краевой, а не угловой элемент. Напротив, подгруппа, состоящая лишь из поворотов верхней грани, не нормальна, так как сопряжения позволяют переместить части верхней грани вниз.
Свойства
Нормальность сохраняется при сюрьективных гомоморфизмах и взятии обратных образов.
Ядро гомоморфизма — нормальная подгруппа.
Нормальность сохраняется при построении прямого произведения.
Нормальная подгруппа нормальной подгруппы не обязана быть нормальной в группе, то есть нормальность не транзитивна. Однако характеристическая подгруппа нормальной подгруппы нормальна.
Каждая подгруппа индекса 2 нормальна. Если
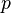 —
наименьший простой делитель порядка
,
то любая подгруппа индекса
нормальна.
—
наименьший простой делитель порядка
,
то любая подгруппа индекса
нормальна.Если — нормальная подгруппа в , то на множестве левых (правых) смежных классов
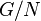 можно
ввести групповую структуру по правилу
можно
ввести групповую структуру по правилу
![]()
Полученное множество называется факторгруппой по .
нормальна тогда и только тогда, когда она тривиально действует на левых смежных классах .
