Представление симметрической группы в виде матричной
Любая подгруппа
группы
перестановок
представима
группой матриц из
,
при этом каждой перестановке
соответствует
матрица, у которой все элементы в ячейках
равны
1, а прочие элементы равны нулю. Например,
перестановка
представляется
следующей матрицей
:
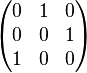
Такие матрицы называются перестановочными
В частности, получаем, что знакопеременная группа - это группа матриц, определитель которых равен 1. Существуют представления симметрических групп меньшей размерности.
14. Знакопеременная группа
Знакопеременной группой подстановок степени n (обозн. ) называется подгруппа симметрической группы степени , содержащая только чётные перестановки.
Свойства
Индекс подгруппы знакопеременной группы в симметрической равен 2:
Знакопеременная группа является нормальной подгруппой симметрической группы (следует из предыдущего утверждения).
Порядок знакопеременной группы равен:
Знакопеременная группа является коммутантом симметрической группы:
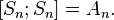
Знакопеременная группа разрешима тогда и только тогда, когда её порядок не больше 4. Точнее,
-
четверной
группе Клейна, а при
.
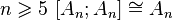15. Циклическая группа
В теории
групп группа
называется
циклической, если она может быть
порождена одним элементом a, то
есть все её элементы являются степенями
a (или, если использовать аддитивную
терминологию, представимы в виде na,
где n — целое
число). Математическое обозначение:
.
Несмотря на своё название, группа не
обязательно должна буквально представлять
собой «цикл». Может случиться так, что
все степени
будут
различными. Порождённая таким образом
группа называется бесконечной
циклической группой и изоморфна
группе целых
чисел по сложению (
).
Свойства
Все циклические группы абелевы.
Каждая конечная циклическая группа изоморфна группе —
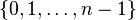со
сложением
по модулю n (её также
обозначают
),
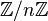а каждая бесконечная — изоморфна
,
группе целых чисел по сложению.
В частности, для каждого натурального числа n существует единственная (с точностью до изоморфизма) циклическая группа порядка n.
Каждая подгруппа циклической группы циклична.
У циклической группы порядка n существует ровно φ(n) порождающих элементов, где φ — функция Эйлера
Если p — простое число, то любая группа порядка p циклическая и единственна с точностью до изоморфизма (это следует из теоремы Лагранжа).
Прямое произведение двух циклических групп порядков и
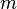циклично
тогда и только тогда, когда n и m
взаимно просты.
Например,
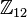изоморфна
,
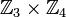но не изоморфна
.
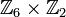Основная теорема о конечнопорождённых абелевых группах утверждает, что любая конечнопорождённая абелева группа единственным образом разлагается в прямое произведение примарных циклических групп. Примарной группой может быть циклическая группа
,
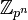где p — простое число, или
.Мультипликативная группа любого конечного поля является циклической (она порождается элементом поля наибольшего порядка).
Кольцо эндоморфизмов группы изоморфно кольцу . При этом изоморфизме числу r соответствует эндоморфизм , который сопоставляет элементу сумму r его экземпляров. Такое отображение будет биекцией, если и только если r взаимно просто с n, так что группа автоморфизмов изоморфна
.
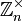Примеры
Группа корней из единицы степени n по умножению.
Группа Галуа любого конечного расширения конечного поля конечна и циклична; обратно, если дано конечное поле F и конечная циклическая группа G, существует конечное расширение F группой Галуа которого будет G.