11. Порядок группы

Пусть — группа, если — конечное множество, то порядком группы называется число элементов и обозначается или . Если — бесконечно, то порядок бесконечен.

12. Смежный класс

СМЕЖНЫЙ КЛАСС группы . но подгруппе Н(л евый) - множество элементов группы G, равное где а - нек-рый фиксированный элемент из G. С. к. наз. также левосторонним С. к. группы G по подгруппе Н, определяемым элементом а. Всякий левый С. к. определяется любым из своих элементов. aН=H тогда и только тогда, когда Для любых С. к. aН и bН либо совпадают, либо не пересекаются. Таким образом, группа G распадается на непересекающиеся левые С. к. по подгруппе Н - это разложение наз. левосторонним разложением группы Gпо подгруппе H. Аналогично определяются правые смежные классы (множества На, ) и правостороннее разложение группы G по подгруппе H. Оба разложения - правостороннее и левостороннее - группы G по Нсостоят из одного и того же числа классов (в бесконечном случае совпадают мощности множеств этих классов). Это число (мощность) наз. индексом подгруппы . в группе G. Для нормальных делителей левостороннее и правостороннее разложения совпадают, и в этом случае говорят просто о разложении группы по ее нормальному делителю.

13. Симметрическая группа

Симметрической группой множества называется группа всех перестановок (то есть биекций ) относительно операции композиции.

Симметрическая группа множества обычно обозначается . Если , то также обозначается через . Но если , то изоморфна , потому при конечном считают, что равно .

Нейтральным элементом в симметрической группе является тождественная перестановка , определяемая как тождественное отображение:

для всех .

Свойства

• При 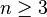симметрическая группа некоммутативна.

• При 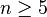симметрическая группа является неразрешимой (и напротив: при 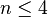— разрешимой).

• В случае, если конечно, число элементов равно 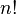(факториал n), где — число элементов . В частности,

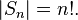
• Каждая конечная группа изоморфна некоторой подгруппе группы 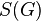(Теорема Кэли).

• Симметрическая группа допускает следующее задание:

(Можно считать, что переставляет и .)

• Максимальный порядок элементов группы - функция Ландау.

• центр симметрической группы тривиален при .

• Симметрическая группа является совершенной (то есть группа её автоморфизмов совпадает с самой группой) тогда и только тогда, когда ее порядок отличен от 2 и 6 (теорема Гёльдера). В случае 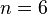группа 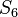имеет еще один внешний автоморфизм. В силу этого и предыдущего свойства при все автоморфизмы являются внутренними, то есть каждый автоморфизм 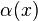имеет вид 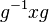для некоторого .

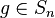• Число классов сопряженных элементов симметрической группы равно числу разбиений числа n.^[2].

• Множество транспозиций 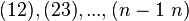является порождающим множеством . С другой стороны, все эти транспозиции порождаются всего двумя перестановками 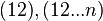, так что минимальное число образующих симметрической группы равно двум.

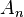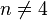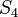• Знакопеременная группа является нормальной подгруппой . Причем - единственная нормальная подгруппа , а при имеет еще одну нормальную подгруппу - четверную группу Клейна.