
- •1. Группоид
- •Типы магм
- •2. Полугруппа
- •Примеры
- •4. Кольцо Определение
- •Простейшие свойства
- •Примеры
- •5. Радикал кольца
- •6. Поле
- •7. Алгебра
- •Свойства
- •8. Кольцо многочленов от нескольких переменных Определение
- •9. Симметрический многочлен
- •10. Порядок элемента группы
- •11. Порядок группы
- •12. Смежный класс
- •13. Симметрическая группа
- •Свойства
- •Представление симметрической группы в виде матричной
- •14. Знакопеременная группа
- •15. Циклическая группа
- •16. Факторгруппа
- •17. Нормальная подгруппа
- •18. Центр группы
- •19. Централизатор элемента группы
- •20. Силовская p-подгруппа
- •Необходимые определения
- •Теоремы
- •Следствие
- •21. Сопряжённый элемент группы
- •22. Идеал кольца
- •23. Главный идеал кольца
- •24. Кольцо главных идеалов
- •25. Сумма идеалов
- •26. Факторкольцо
- •27. Характеристика поля
- •28. Представление Определения и концепции
- •Определение
- •29. Модуль
- •30. Примитивный элемент
- •31. Тело
- •32. Алгебраическая система
- •Основные классы алгебраических систем
- •Группоиды, полугруппы, группы
- •Алгебры
- •33. Многообразие
- •35. Дистрибутивная решётка
- •36. Булева алгебра
- •37. Фильтр
- •Определение в рамках теории решёток
- •Фильтры на множествах
- •База фильтра
- •Сравнение фильтров
- •Фильтры в топологических пространствах
- •Примеры
- •38. Ультрафильтр
- •39. Ультрапроизведение
7. Алгебра
Алгебра (универсальная алгебра) —
множество
![]() ,
называемое носителем алгебры,
снабжённое набором
,
называемое носителем алгебры,
снабжённое набором
![]() -арных
алгебраических
операций на
,
называемым сигнатурой, или структурой
алгебры. Иными словами, универсальной
алгеброй является алгебраическая
система с пустым множеством
отношений.
-арных
алгебраических
операций на
,
называемым сигнатурой, или структурой
алгебры. Иными словами, универсальной
алгеброй является алгебраическая
система с пустым множеством
отношений.
Свойства
Для универсальных алгебр имеет место
теорема о гомоморфизме: если
![]() —
гомоморфизм
алгебр, а
—
гомоморфизм
алгебр, а
![]() —
ядерная конгруэнция
—
ядерная конгруэнция
![]() (то
есть
(то
есть
![]() ,
то факторалгебра
,
то факторалгебра
![]() изоморфна
изоморфна
![]() .
.
Для универсальных алгебр исследованы
сопутствующие структуры: группа
автоморфизмов
![]() ,
моноид
эндоморфизмов
,
моноид
эндоморфизмов
![]() ,
решётка
подалгебр
,
решётка
подалгебр
![]() ,
решётка конгруэнций
,
решётка конгруэнций
![]() ,
в частности, показано, что для любой
группы
и
решёток
,
в частности, показано, что для любой
группы
и
решёток
![]() и
и
![]() существует
такая универсальная алгебра
,
что
существует
такая универсальная алгебра
,
что
![]() ,
,
![]() ,
,
![]() .
.
Универсальная алгебра с одной бинарной алгебраической операцией называется группоидом (магмой).
8. Кольцо многочленов от нескольких переменных Определение
Многочлен от n переменных X1,…, Xn с коэффициентами в поле K определяется аналогично многочлену от одной переменной, но обозначения становятся более сложными. Для любого мультииндекса α = (α1,…, αn), где каждое αi — ненулевое целое число, пусть

Xα называется одночленом
степени
![]() .
Многочлен — это конечная линейная
комбинация одночленов с коэффициентами
в K:
.
Многочлен — это конечная линейная
комбинация одночленов с коэффициентами
в K:
![]() .
.
Многочлены от n переменных с коэффициентами в поле k (с обычными операциями сложения и умножения) образуют коммутативное кольцо, обозначаемое k[x1,…, xn]. Это кольцо можно получить многократным применением операции «взятие кольца многочленов над данным кольцом». Например, k[x1, x2] изоморфно k[x1][x2], как и k[x2][x1]. Это кольцо игрет фундаментальную роль в алгебраической геометрии. Многие результаты коммутативной алгебры были достигнуты благодаря изучению идеалов этого кольца и модулей над ним.
9. Симметрический многочлен
Симметри́ческий многочле́н —
многочлен
от n переменных
![]() ,
не изменяющийся при всех перестановках
входящих в него переменных.
,
не изменяющийся при всех перестановках
входящих в него переменных.
Примеры
Дискриминант — многочлен вида
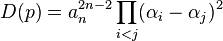 ,
где
,
где
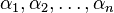 —
корни некого многочлена от одной
переменной:
—
корни некого многочлена от одной
переменной:
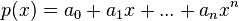 .
.
Степенные суммы — суммы одинаковых степеней переменных, то есть

Основные симметрические многочлены — многочлены вида
![]()
определённые для
![]() ,
то есть такие:
,
то есть такие:
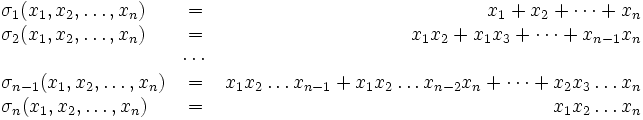
10. Порядок элемента группы
Описание
Пусть
![]() —
группа
и
—
группа
и
![]() —
элемент группы.
—
элемент группы.
Определение 1. Говорят, что
![]() имеет
порядок1)
имеет
порядок1)
![]() ,
если
,
если
![]() —
наименьшее положительное число такое,
что
—
наименьшее положительное число такое,
что
![]() ,
то есть
,
то есть
![]() .
Если такого положительного
не
существует, то говорят, что
имеет
бесконечный порядок2).
Порядок единичного
элемента
.
Если такого положительного
не
существует, то говорят, что
имеет
бесконечный порядок2).
Порядок единичного
элемента
![]() считается
равным нулю.
считается
равным нулю.
Предложение 1. Пусть
![]() —
конечная группа и
—
некоторый ее элемент. Тогда
—
конечная группа и
—
некоторый ее элемент. Тогда
![]() делит
порядок
группы
.
делит
порядок
группы
.
Примеры
В множестве целых чисел
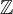 любой
ненулевой элемент имеет бесконечный
порядок.
любой
ненулевой элемент имеет бесконечный
порядок.В группе классов вычетов
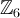 элементы
элементы
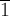 и
и
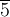 имеют
порядок 6, элементы
имеют
порядок 6, элементы
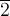 и
и
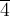 —
порядок 3, элемент
—
порядок 3, элемент
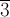 —
порядок 2.
—
порядок 2.
Определение: |
Порядком элемента
|
Порядок любого ненулевого элемента в группе целых чисел по сложению равен бесконечности.
Порядок элемента
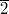 в
группе вычетов по модулю
в
группе вычетов по модулю
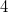 конечен
и равен двум, поскольку
конечен
и равен двум, поскольку
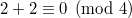 .
.
Утверждение: |
В конечной группе у всех элементов конечный порядок. |
|
Действительно, необходимо при некоторых
|
|
Определение: |
|
Группа вычетов по модулю простого числа относительно сложения:
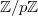 .
.
Циклическая группа порядка
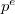 .
.
