
- •1. Группоид
- •Типы магм
- •2. Полугруппа
- •Примеры
- •4. Кольцо Определение
- •Простейшие свойства
- •Примеры
- •5. Радикал кольца
- •6. Поле
- •7. Алгебра
- •Свойства
- •8. Кольцо многочленов от нескольких переменных Определение
- •9. Симметрический многочлен
- •10. Порядок элемента группы
- •11. Порядок группы
- •12. Смежный класс
- •13. Симметрическая группа
- •Свойства
- •Представление симметрической группы в виде матричной
- •14. Знакопеременная группа
- •15. Циклическая группа
- •16. Факторгруппа
- •17. Нормальная подгруппа
- •18. Центр группы
- •19. Централизатор элемента группы
- •20. Силовская p-подгруппа
- •Необходимые определения
- •Теоремы
- •Следствие
- •21. Сопряжённый элемент группы
- •22. Идеал кольца
- •23. Главный идеал кольца
- •24. Кольцо главных идеалов
- •25. Сумма идеалов
- •26. Факторкольцо
- •27. Характеристика поля
- •28. Представление Определения и концепции
- •Определение
- •29. Модуль
- •30. Примитивный элемент
- •31. Тело
- •32. Алгебраическая система
- •Основные классы алгебраических систем
- •Группоиды, полугруппы, группы
- •Алгебры
- •33. Многообразие
- •35. Дистрибутивная решётка
- •36. Булева алгебра
- •37. Фильтр
- •Определение в рамках теории решёток
- •Фильтры на множествах
- •База фильтра
- •Сравнение фильтров
- •Фильтры в топологических пространствах
- •Примеры
- •38. Ультрафильтр
- •39. Ультрапроизведение
5. Радикал кольца
Правило
![]() ,
сопоставляющее каждому кольцу
,
сопоставляющее каждому кольцу
![]() некоторый
идеал
некоторый
идеал
![]() ,
такой что
,
такой что
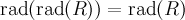 ;
; ;
;для любого гомоморфизма колец
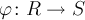 имеет
место включение
имеет
место включение
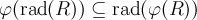 ,
,
называется радикалом1) кольца.
Для кольца идеалом называется подкольцо, замкнутое относительно умножения на элементы из . При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из . Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.
Более точно: Идеалом кольца
называется
такое подкольцо
![]() кольца
,
что
кольца
,
что
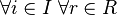 произведение
произведение
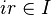 (условие
на правые идеалы);
(условие
на правые идеалы);произведение
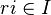 (условие
на левые идеалы).
(условие
на левые идеалы).
Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры.
РАДИКАЛ ИДЕАЛА
Радикал
идеала I — это множество
![]() .
Оно тоже является идеалом кольца A,
если только кольцо A коммутативно.
В случае, когда I=(0), этот идеал
называется нильрадикалом
кольца A. Его элементами являются
все нильпотентные элементы кольца. Если
коммутативное кольцо не имеет нильпотентных
элементов, кроме нуля, (имеет нулевой
нильрадикал), — оно называется
радикальным. Идеал I называется
радикальным, если он совпадает со своим
радикалом. В этом случае факторкольцо
R/I не имеет нильпотентных элементов,
кроме нуля.
.
Оно тоже является идеалом кольца A,
если только кольцо A коммутативно.
В случае, когда I=(0), этот идеал
называется нильрадикалом
кольца A. Его элементами являются
все нильпотентные элементы кольца. Если
коммутативное кольцо не имеет нильпотентных
элементов, кроме нуля, (имеет нулевой
нильрадикал), — оно называется
радикальным. Идеал I называется
радикальным, если он совпадает со своим
радикалом. В этом случае факторкольцо
R/I не имеет нильпотентных элементов,
кроме нуля.
6. Поле
По́лем называется множество
F с двумя бинарными
операциями
![]() (аддитивная
операция или сложение) и
(аддитивная
операция или сложение) и
![]() (мультипликативная
операция или умножение), если оно
(вместе с этими операциями) образует
коммутативное ассоциативное кольцо
c единицей, все ненулевые
элементы которого обратимы.
(мультипликативная
операция или умножение), если оно
(вместе с этими операциями) образует
коммутативное ассоциативное кольцо
c единицей, все ненулевые
элементы которого обратимы.
Иными словами, множество F с двумя бинарными операциями (сложение) и (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.
Характеристика поля всегда 0 или простое число.
Поле характеристики 0 содержит
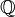 ,
поле рациональных чисел.
,
поле рациональных чисел.
Поле характеристики p содержит
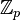 ,
поле вычетов по модулю
,
поле вычетов по модулю
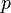 .
.
Количество элементов в конечном поле всегда равно
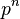 ,
степени простого числа.
,
степени простого числа.
При этом для любого числа вида существует единственное (с точностью до изоморфизма) поле из элементов, обычно обозначаемое
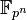 .
.
Любой гомоморфизм полей является вложением.
Примеры
— рациональные числа,
![]() —
вещественные
числа,
—
вещественные
числа,
![]() —
комплексные
числа,
—
комплексные
числа,
— поле вычетов по модулю p, где p — простое число.
![]() —
конечное
поле из
—
конечное
поле из
![]() элементов,
где p — простое число, k —
натуральное.
элементов,
где p — простое число, k —
натуральное.
Дистрибути́вность (от латинского distributivus — «распределительный») — свойство согласованности двух бинарных операций, определённых на одном и том же множестве.
Говорят, что две бинарные операции + и
× удовлетворяют свойству дистрибутивности,
если для любых трех элементов
![]() :
:
![]() —
дистрибутивность слева;
—
дистрибутивность слева;
![]() —
дистрибутивность справа.
—
дистрибутивность справа.
