Примеры

• Множество всех окрестностей точки топологического пространства является фильтром;

• Если  — бесконечное множество, то множество дополнений конечных множеств является фильтром. Такой фильтр называется коконечным фильтром или фильтром Фреше.

• Если  — бесконечное множество мощност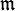и , то множество дополнений множеств мощности 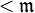тоже является фильтром.

38. Ультрафильтр

Ультрафильтр на решётке  — это максимальный собственный фильтр. Понятие ультрафильтра появилось в общей топологии, где оно используется для обобщения понятия сходимости на пространства с несчётной базой.

Определение

Собственный фильтр на решётке является ультрафильтром, если он не содержится ни в одном собственном (т.е. отличном от ) фильтре.

Набор подмножеств множества называется ультрафильтром на , если

• 

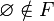
• для любых двух элементов , их пересечение также лежит в

• для любого элемента , все его надмножества лежат в

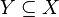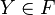• для любого подмножества либо , либо

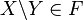
Иначе говоря, если рассмотреть функцию на множествах , заданную как , если , и в противном случае, то является конечно-аддитивной вероятностной мерой на .

Ультрафильтры в булевых алгебрах

Если решётка является булевой алгеброй, то возможна следующая характеризация ультрафильтров: фильтр является ультрафильтром тогда и только тогда, когда для любого элемента либо , либо

Эта характеризация делает ультрафильтры похожими на полные теории.

Примеры

• любой главный фильтр является ультрафильтром

• подмножество алгебры Линденбаума — Тарского полной теории 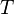, состоящее из теорем

Свойства

• ультрафильтр на конечном множестве всегда является главным.

• любой ультрафильтр на бесконечном множестве содержит конечный фильтр.

• если — главный ультрафильтр на множестве , то его главный элемент является пересечением всех элементов ультрафильтра.

• если — неглавный ультрафильтр на множестве , то пересечение всех его элементов пусто.

39. Ультрапроизведение

Пусть  — язык.  — семейство алгебраических систем, . Прямым произведением алгебраических систем , , называется алгебраическая система 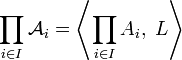, где для каждого предикатного символа

для каждого ;

для каждого функционального символа

и для каждого константного символа

Пусть  — фильтр над . Определим на отношение . Введём обозначения:

,

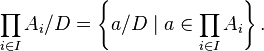
Определим алгебраическую систему 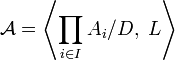следующим образом.

Положим для предикатного символа

для каждого функционального символа

и для константных символов

Определённая таким образом алгебраическая система называется фильтрованным произведением систем по фильтру и обозначается . Если  — ультрафильтр, то называется ультрапроизведением, если все совпадают и равны , то называется ультрастепенью и обозначается .

Основное свойство ультрапроизведений состоит в том, что они сохраняют все предложения:

Теорема Лося. Пусть  — язык,  — семейство алгебраических систем языка ,  — ультрафильтр над . Тогда для любой формулы языка и любой последовательности элементов из

Также теорему компактности можно сформулировать следующим образом.

Теорема компактности. Если множество формул локально выполнимо в некотором классе , то оно выполнимо в некотором ультрапроизведении систем из