37. Фильтр

Фильтр — подмножество решётки, удовлетворяющее определённым условиям. Понятие происходит из общей топологии, где возникают фильтры на решётке всех подмножеств какого-либо множества, упорядоченных отношением включения. Фильтр — понятие, двойственное идеалу.

Определение в рамках теории решёток

Подмножество решётки называется фильтром, если

• для всех ,

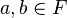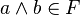
• для всех 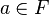и таких, что ,

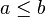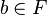
Фильтр называется собственным, если .

Собственный фильтр такой, что не существует других собственных фильтров, его содержащих, называется ультрафильтром или максимальным фильтром.

Фильтр называется простым, если в нём для всех из того, что , следует, что либо , либо .

Минимальный фильтр, содержащий данный элемент , называется главным фильтром, сгенерированным главным элементом .

Если фильтр, то является идеалом.

Фильтры на множествах

Частным случаем фильтра является фильтр на множестве. Для каждого множества можно определить решётку его подмножеств . Тогда фильтр на определяется как подмножество , удовлетворяющее следующим условиям:

• 

• 

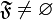
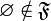
• пересечение любых двух элементов лежит в

• надмножество любого элемента лежит в

Фильтр вида называется фильтром, порожденным множеством . Фильтр, порожденный множеством из одного элемента, называется главным. Главный фильтр является ультрафильтром.

База фильтра

Пусть — фильтр на множестве . Семейство подмножеств называется базой (базисом) фильтра , если любой элемент фильтра содержит некоторый элемент базы , т.е. для любого существует такое, что . При этом фильтр совпадает с семейством всевозможных надмножеств множеств из . В частности, фильтры, имеющие общую базу, совпадают. Говорят также, что база порождает фильтр

Для того, чтобы семейство подмножеств множества являлось базой некоторого фильтра на необходимо и достаточно выполнение следующих условий (аксиом базы):

• ;

• ;

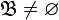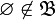• для любых 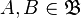существует 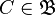такое, что .

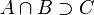Две базы и называются эквивалентными, если любой элемент содержит в себе некоторый элемент , и наоборот, любой элемент содержит в себе некоторый элемент .

Эквивалентные базы порождают один и тот же фильтр. Среди всех баз, эквивалентных данной базе существует максимальная по включению база, а именно, порождаемый этой базой фильтр . Таким образом, между классами эквивалентных баз и фильтрами существует естественное взаимно-однозначное соответствие.

Сравнение фильтров

Пусть на множестве заданы два фильтра и . Говорят, что фильтр мажорирует фильтр ( сильнее , тоньше ), если . В этом случае также говорят, что фильтр мажорируется фильтром ( слабее , грубее ).

Говорят, что база сильнее базы , и записывают , если любой элемент содержит в себе некоторый элемент . База сильнее базы тогда и только тогда, когда фильтр , порожденный базой , сильнее фильтра , порожденного базой .

Базы и эквивалентны тогда и только тогда, когда одновременно и .

Фильтры в топологических пространствах

Пусть — топологическое пространство и — фильтр на множестве . Точка называется пределом фильтра , если любая окрестность точки принадлежит фильтру . Обозначение: . Для фильтра , порожденного базой , равенство выполняется тогда и только тогда, когда любая окрестность целиком содержит некоторое множество из .

В хаусдорфовом топологическом пространстве фильтр может иметь не более одного предела.

Точка называется предельной точкой (точкой прикосновения, частичным пределом) фильтра , если принадлежит замыканию любого множества из , т.е. для всех . Равносильно, для любой окрестности точки и для любого выполнено . Любая предельная точка ультрафильтра является его пределом.

В компактном топологическом пространстве любой фильтр имеет предельную точку, а любой ультрафильтр имеет предел.