Алгебры

• Алгебра (линейная) — пространство с билинейной дистрибутивной операцией умножения, иначе говоря, кольцо с согласованной структурой пространства

• Ассоциативная алгебра — алгебра с ассоциативным умножением

• Алгебра термов

• Коммутативная алгебра

• Градуированная алгебра

• Алгебра Ли — алгебра с антикоммутативным умножением (обычно обозначаемым 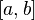), удовлетворяющим тождеству Якоби

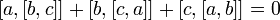
• Алгебра Лейбница — алгебра с умножением (обычно обозначаемым ), удовлетворяющим тождеству Якоби

• Алгебра Йордана — коммутативная алгебра с тождеством слабой ассоциативности:

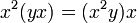
• Алгебра некоммутативная йорданова — некоммутативная алгебра с тождеством слабой ассоциативности: и тождеством эластичности:

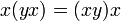
• Альтернативная алгебра — алгебра с тождествами

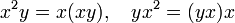
• Алгебра Мальцева — антикоммутативная алгебра с тождеством:

• Коммутантно-ассоциативная алгебра

• Алгебра над операдой — один из наиболее общих видов алгебраических систем. Здесь сама операда играет роль сигнатуры алгебры.

Решётки

• Решётка — структура с двумя коммутативными, ассоциативными, идемпотентными операциями, удовлетворяющими закону поглощения.

• Булева алгебра.

33. Многообразие

Линейным многообразием в линейном пространстве называется подмножество этого пространства вида

для каких-то фиксированных подпространства и вектора , то есть подмножество, полученное сдвигом каждого элемента из на вектор . Обозначение:

Если и , то тогда и только тогда, когда и .

В частности, является линейным подпространством тогда и только тогда, когда (т.е. содержит нулевой элемент). В этом случае .

Если — гильбертово пространство, а — его замкнутое подпространство, то можно выбрать вектор в определении ( ) ортогональным подпространству . Такое представление , единственно.

Пересечение линейных многообразий всегда является линейным многообразием.

Размерность линейного многообразия — это размерность линейного подпространства : Для линейных многообразий в -мерном векторном пространстве или , или

АЛГЕБРАИЧЕСКИХ СИСТЕМ МНОГООБРАЗИЕ

алгебраических систем класс фиксированной сигнатуры и, аксиоматизируемый при помощи тождеств, т. е. формул вида

где - к.-л. предикатный символ из или знак равенства, а - термы сигнатуры Q от предметных переменных А. с. м. наз. иначе э к, вациональными классами, иногда примитивными классами. Многообразие сигнатуры может быть определено также (теорема Биркгофа) как непустой класс -систем, замкнутый относительно подсистем, гомоморфных образов и декартовых произведений.

Пересечение всех многообразий сигнатуры , содержащих данный (не обязательно абстрактный) класс -систем, наз. эквациональным замыканием класса (или многообразием, порожденным классом > и обозначается . В частности, если класс состоит из одной -системы , то его эквацп-ональное замыкание обозначают . Если система конечна, то все конечно порожденные системы в многообразии также конечны [1], [2].

Пусть - нек-рый класс -систем, - класс подсистем систем из - класс гомоморфных образов систем из - класс изоморфных копий декартовых произведений систем пз . Для произвольного непустого класса -систем имеет место соотношение (см. [1], [2]):

34. РЕШЁТКА

Решётка (ранее использовался термин структура) — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.

Примеры

1. множество всех подмножеств данного множества, упорядоченное по включению; например: ;

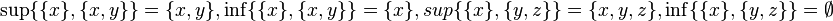2. всякое линейно упорядоченное множество; причём если 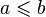, то ;

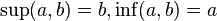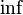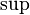3. множество всех подпространств векторного пространства, упорядоченных по включению, где  — пересечение, а  — сумма соответствующих подпространств;

4. множество всех неотрицательных целых чисел, упорядоченных по делимости: , если 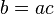для некоторого . Здесь  — наименьшее общее кратное, а  — наибольший общий делитель данных чисел;

5. вещественные функции, определённые на отрезке [0, 1], упорядоченные условием 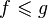, если 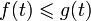для всех 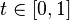. Здесь

, где .

Алгебраическое определение

Решётка может быть также определена как универсальная алгебра с двумя бинарными операциями (они обозначаются и или + и ∙), удовлетворяющая следующим тождествам

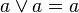
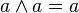1. (идемпотентность)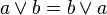

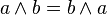2. (коммутативность)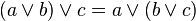

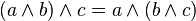3. (ассоциативность)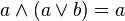

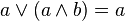4. (поглощение).

Связь между этими двумя определениями устанавливается при помощи формул:

,

,

и обратно. При этом для любых элементов и эквивалентны следующие утверждения:

;

;

.

Понятия изоморфизма решёток как универсальных алгебр и как частично упорядоченных множеств совпадают. Однако произвольное изотонное отображение решётки в решётку не обязано быть гомоморфизмом этих решёток как универсальных алгебр.