31. Тело

Те́ло — множество с двумя операциями (сложение и умножение), обладающее следующими свойствами:

• образует абелеву группу относительно сложения;

• все ненулевые элементы образуют группу относительно умножения;

• имеет место дистрибутивность умножения относительно сложения.

Если умножение коммутативно, тело называется полем.

Свойства

• Теорема Веддербёрна: всякое конечное тело является полем.

Примеры

• Тело кватернионов .

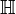32. Алгебраическая система

Алгебраическая система (или алгебраическая структура) в универсальной алгебре — множество (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений называется алгеброй, а система с пустым множеством операций — моделью.

n-арная операция на G — это отображение прямого произведения n экземпляров множества в само множество . По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).

Для алгебраических систем естественным образом определяются морфизмы как отображения, сохраняющие операцию. Таким образом определяются категории групп, колец, R-модулей и т. п.

Если множество обладает структурой топологического пространства, и операции являются непрерывными, то его называют топологической алгебраической системой. Так, в топологической группе операции умножения и взятия обратного элемента являются непрерывными.

Не все алгебраические конструкции описываются алгебраическими системами, в качестве примера таковых можно упомянуть коалгебры, биалгебры, алгебры Хопфа и комодули над ними.

Основные классы алгебраических систем

• Множество можно считать вырожденной алгебраической системой с пустым набором операций и отношений^[1].

Группоиды, полугруппы, группы

• Группоид — множество с одной бинарной операцией 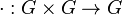, обычно называемой умножением.

• Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение 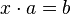имеет единственное решение для любых и .

• Квазигруппа — одновременно правая и левая квазигруппы.

• Лупа — квазигруппа с единичным элементом 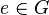, таким, что .

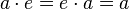• Полугруппа — группоид, в котором умножение ассоциативно: .

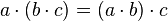• Моноид — полугруппа с единичным элементом.

• Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a⁻¹, такой, что .

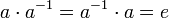• Абелева группа — группа, в которой операция коммутативна, то есть, 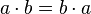. Операцию в абелевой группе часто называют сложением ('+').

Кольца

• Полукольцо — похоже на кольцо, но без обратимости сложения.

• Почти-кольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)

• Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон дистрибутивности: .

• Коммутативное кольцо — кольцо с коммутативным умножением.

• Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.

• Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.

• Поле — коммутативное кольцо, являющееся телом.