29. Модуль

Мо́дуль над кольцо́м — одно из основных понятий в общей алгебре, являющееся обобщением двух алгебраических понятий — векторного пространства (фактически, векторное пространство — это модуль над полем), и абелевой группы (которая является модулем над кольцом целых чисел ).

Понятие модуля лежит в основе коммутативной алгебры, которая играет важную роль в различных областях математики, таких как

• алгебраическая геометрия,

• гомологическая алгебра,

• теория представлений групп.

Мотивировка

В векторном пространстве множество скаляров образует поле и умножение на скаляр удовлетворяет нескольким аксиомам, таким как дистрибутивность умножения. В модуле же требуется только, чтобы скаляры образовывали кольцо (ассоциативное с единицей), аксиомы же остаются теми же самыми.

Значительная часть теории модулей состоит из попыток обобщить на них известные свойства векторных пространств, иногда для этого приходится ограничиваться модулями над «хорошо ведущими себя» кольцами, такими как области главных идеалов. Однако в целом модули устроены более сложно, чем векторные пространства. Например, не в каждом модуле можно выбрать базис, и даже те, в которых это возможно могут иметь несколько базисов с различным числом элементов (в случае некоммутативного кольца).

Определения

Пусть  — кольцо (как правило, считающееся коммутативным c единичным элементом). -модулем называется абелева группа с операцией умножения на элементы кольца

которая удовлетворяет следующим условиям:

1)

2)

3)

4)

Примечание: В случае некоммутативного кольца такие модули часто называются левыми. Правыми модулями называют в этом случае такие объекты, у которых условие 1) заменено следующим:

что гораздо удобнее формулировать, записывая элемент кольца при умножении справа от элемента модуля:

отсюда и терминология.

В случае коммутативного кольца R определения левого и правого модуля совпадают и их называют просто модулями.

Любое кольцо R можно рассматривать как модуль над собой (в некоммутативном случае оно является также правым модулем над собой).

Примеры

• Любая абелева группа — модуль над кольцом целых чисел.

• Линейное пространство над полем 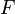является модулем над .

• Линейное пространство 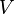 — модуль над кольцом всех своих линейных преобразований

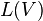
• Дифференциальные формы на гладком многообразии снабжены естественной структурой модуля над кольцом всех гладких функций на .

• Если I — левый идеал кольца R, он будет левым модулем над этим кольцом. Аналогично, правые идеалы будут правыми модулями.

30. Примитивный элемент

Примитивным элементом конечного поля называется всякий первообразный корень степени , то есть всякий генератор мультипликативной группы этого поля.

Свойства

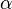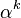• Если — примитивный элемент поля , то любой другой примитивный элемент может быть получен как степень , где k — целое число, взаимно простое с . Поэтому количество различных примитивных элементов в поле равно значению функции Эйлера .

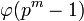• Минимальный многочлен примитивного элемента поля называется примитивным многочленом над полем .
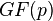