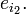- •1. Группоид
- •Типы магм
- •2. Полугруппа
- •Примеры
- •4. Кольцо Определение
- •Простейшие свойства
- •Примеры
- •5. Радикал кольца
- •6. Поле
- •7. Алгебра
- •Свойства
- •8. Кольцо многочленов от нескольких переменных Определение
- •9. Симметрический многочлен
- •10. Порядок элемента группы
- •11. Порядок группы
- •12. Смежный класс
- •13. Симметрическая группа
- •Свойства
- •Представление симметрической группы в виде матричной
- •14. Знакопеременная группа
- •15. Циклическая группа
- •16. Факторгруппа
- •17. Нормальная подгруппа
- •18. Центр группы
- •19. Централизатор элемента группы
- •20. Силовская p-подгруппа
- •Необходимые определения
- •Теоремы
- •Следствие
- •21. Сопряжённый элемент группы
- •22. Идеал кольца
- •23. Главный идеал кольца
- •24. Кольцо главных идеалов
- •25. Сумма идеалов
- •26. Факторкольцо
- •27. Характеристика поля
- •28. Представление Определения и концепции
- •Определение
- •29. Модуль
- •30. Примитивный элемент
- •31. Тело
- •32. Алгебраическая система
- •Основные классы алгебраических систем
- •Группоиды, полугруппы, группы
- •Алгебры
- •33. Многообразие
- •35. Дистрибутивная решётка
- •36. Булева алгебра
- •37. Фильтр
- •Определение в рамках теории решёток
- •Фильтры на множествах
- •База фильтра
- •Сравнение фильтров
- •Фильтры в топологических пространствах
- •Примеры
- •38. Ультрафильтр
- •39. Ультрапроизведение
27. Характеристика поля
Характеристика
поля — наименьшее положительное
целое
![]() число
такое, что сумма
копий
единицы равна нулю:
число
такое, что сумма
копий
единицы равна нулю:
![]() Если
такого числа не существует то характеристика
равна 0 по определению.
Если
такого числа не существует то характеристика
равна 0 по определению.
Характеристика поля всегда 0 или простое число.
Поле характеристики 0 содержит , поле рациональных чисел.
Поле характеристики p содержит , поле вычетов по модулю .
ХАРАКТЕРИСТИКА ПОЛЯ
целое положительное простое число или число 0, однозначно определяемое для данного поля следующим образом. Если для нек-рого п>0
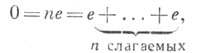 где
е - единица поля К, то наименьшее из
таких пбудет простым числом и оно наз.
характеристикой поля К. Если же
такого числа не существует, то говорят,
что X. п. Кравна нулю, или что К - поле
нулевой характеристики. Иногда такое
поле наз. полем без характеристики или
полем бесконечной
где
е - единица поля К, то наименьшее из
таких пбудет простым числом и оно наз.
характеристикой поля К. Если же
такого числа не существует, то говорят,
что X. п. Кравна нулю, или что К - поле
нулевой характеристики. Иногда такое
поле наз. полем без характеристики или
полем бесконечной
![]() характеристики.
Всякое поле нулевой характеристики
содержит подполе, изоморфное полю всех
рациональных чисел, а поле конечной
характеристики р - подполе, изоморфное
полю классов вычетов по модулю р.
характеристики.
Всякое поле нулевой характеристики
содержит подполе, изоморфное полю всех
рациональных чисел, а поле конечной
характеристики р - подполе, изоморфное
полю классов вычетов по модулю р.
28. Представление Определения и концепции
Пусть V — векторное пространство над полем F. Для примера, предположим, что V — это Rn или Cn, стандартное n-мерное пространство векторов-столбцов над полем вещественных или комплексных чисел соответственно. В данном случае идея теории представлений заключается в том, чтобы конкретизировать абстрактную алгебру использованием матриц n × n, элементами которых являются вещественные или комплексные числа.
Существует три вида алгебраических объектов, для которых это возможно: группы, ассоциативные алгебры и алгебры Ли.
Множество всех обратимых матриц n × n является группой по умножению матриц, и теория представлений групп анализирует группу, описывая (представляя) её элементы терминами обратимых матриц.
Сложение и умножение матриц делает множество всех матриц n × n ассоциативной алгеброй, и, следовательно, есть соответствующая теория представлений ассоциативных алгебр.
Если мы заменим матричное умножение MN матричным коммутатором MN — NM, то матрицы n × n заменят алгебру Ли, что приводит к созданию теории представлений алгебр Ли.
Это обобщается на любое поле F и любое векторное пространство V над F с заменой линейных отображений матрицами и заменой композиции отображений матричным умножением: получим группу GL(V,F) автоморфизмов над V, ассоциативную алгебру EndF(V) всех эндоморфизмов над V и соответствующую алгебру Ли gl(V,F).
Определение
Существует два способа определить представление. Первый использует идею действия группы, обобщая способ матрицы воздействовать на вектор-столбец с помощью матричного умножения. Представление группы G или алгебры A (ассоциативной или Ли) на векторном пространстве V — это отображение
![]()
с двумя свойствами. Во-первых, для любых g из G (или a из A), отображение
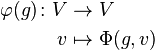
линейно (над F).
В зависимости от представленной группы различают разделы теории представлений:
конечные группы — См. Теория представлений конечных групп.
топологические группы — некоторые построения для представлений конечных групп можно обобщить и для бесконечных групп. Для локально компактных топологических групп это можно сделать с помощью меры Хаара. На результирующей теории во многом основан гармонический анализ, а также современное изложение общей теории Фурье.
группы Ли — многие группы Ли являются компактными. Соответственно к ним можно применить теорию представлений компактных групп.
Представле́ние гру́ппы (точнее, линейное представление группы) — гомоморфизм заданной группы в группу невырожденных линейных преобразований векторного пространства.
Определение
Пусть
—
заданная группа и
![]() —
векторное пространство. Тогда представление
группы
—
это отображение, ставящее в соответствие
каждому элементу
—
векторное пространство. Тогда представление
группы
—
это отображение, ставящее в соответствие
каждому элементу
![]() невырожденное
линейное преобразование
невырожденное
линейное преобразование
![]() причем
выполняются свойства
причем
выполняются свойства
![]()
Раздел математики, который изучает представления групп, называется теорией представлений (групп). Представление можно понимать как запись группы с помощью матриц или преобразований линейного пространства. Смысл использования представлений групп заключается в том, что задачи из теории групп сводятся к более наглядным задачам из линейной алгебры. Этим объясняется большая роль теории представлений в различных вопросах алгебры и других разделов математики. Например, одномерные представления симметрической группы и знакопеременной группы играют большую роль при доказательстве невозможности разрешения в радикалах алгебраического уравнения степени выше 4. В квантовой механике важную роль играют бесконечномерные (в которых векторное пространство — гильбертово) представления групп (в первую очередь, группы Лоренца).
Типы представлений
Представление называется точным, если ядро соответствующего гомоморфизма состоит лишь из единичного элемента.
Представление группы называется приводимым, если в векторном пространстве есть подпространство, отличное от нулевого и самого
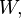 инвариантное
для всех преобразований
инвариантное
для всех преобразований
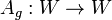
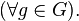 В
противном случае представление
называется неприводимым или простым.
Теорема
Машке утверждает, что конечномерные
представления конечных
групп над полем характеристики
ноль (или положительной, но не делящей
порядок
группы) всегда раскладываются в прямую
сумму неприводимых.
В
противном случае представление
называется неприводимым или простым.
Теорема
Машке утверждает, что конечномерные
представления конечных
групп над полем характеристики
ноль (или положительной, но не делящей
порядок
группы) всегда раскладываются в прямую
сумму неприводимых.Всякое неприводимое представление коммутативной группы над полем комплексных чисел одномерно. Такие представления называются характерами.
Представление называется регулярным, если — пространство функций на группе и линейное преобразование
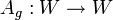 ставит
в соответствие каждой функции
ставит
в соответствие каждой функции
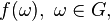 функцию
функцию
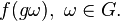
Представление называется унитарным относительно некоторого эрмитова скалярного произведения в пространстве над полем
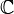 ,
если все преобразования
,
если все преобразования
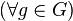 являются
унитарными.
Представление называется унитаризуемым,
если в векторном пространстве
(над
полем
)
множно ввести такое эрмитово скалярное
произведение, относительно которого
оно является унитарным. Любое представление
конечной группы
унитаризуемо:
достаточно выбрать в пространстве
произвольное
эрмитово скалярное произведение
и
определить искомое эрмитово скалярное
произведение формулой
являются
унитарными.
Представление называется унитаризуемым,
если в векторном пространстве
(над
полем
)
множно ввести такое эрмитово скалярное
произведение, относительно которого
оно является унитарным. Любое представление
конечной группы
унитаризуемо:
достаточно выбрать в пространстве
произвольное
эрмитово скалярное произведение
и
определить искомое эрмитово скалярное
произведение формулой
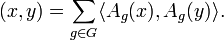
Если ― топологическая группа, то под представлением обычно понимается непрерывное линейное представление группы в топологическом векторном пространстве.
Примеры
Унитарная группа U(1) может быть представлена как группа вращений двумерного пространства вокруг центра.
Представление симметрической группы может быть получено следующим образом. Выберем в векторном пространстве размерности базис
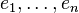 .
Для каждой перестановки
.
Для каждой перестановки
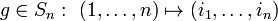 определим
линейное преобразование
переводящее
базисный вектор
определим
линейное преобразование
переводящее
базисный вектор
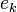 в
базисный вектор
в
базисный вектор
 где
где
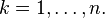 Таким
образом получается
-мерное
представление группы
Таким
образом получается
-мерное
представление группы
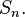
Неприводимое двумерное представление группы
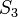 можно
получить, выбрав в плоскости
базис
можно
получить, выбрав в плоскости
базис
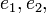 положив
вектор
положив
вектор
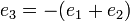 и
определив для каждой перестановки
и
определив для каждой перестановки
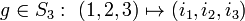 линейное
преобразование
,
переводящее
линейное
преобразование
,
переводящее
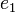 в
в
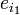 и
и
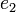 в
в