22. Идеал кольца

Для кольца идеалом называется подкольцо, замкнутое относительно умножения на элементы из . При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из . Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.

Более точно: Идеалом кольца называется такое подкольцо кольца , что

1. произведение (условие на правые идеалы);

2. произведение (условие на левые идеалы).

Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры.

Свойства

• Левые идеалы в R являются правыми идеалами в т.н. противоположном кольце — кольце с теми же элементами и тем же сложением, что и данное, но с умножением определенным 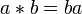, и наоборот.

• Двусторонние идеалы в кольцах и алгебрах играют ту же роль, что и нормальные подгруппы в группах:

  • Для всякого гомоморфизма 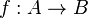ядром 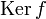является идеал, и обратно, всякий идеал — ядро некоторого гомоморфизма.

  • Более того, идеал однозначно (с точностью до изоморфизма) определяет образ гомоморфизма, ядром которого он является: 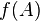изоморфен факторкольцу (факторалгебре) .

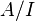• В кольце целых чисел все идеалы главные и имеют вид 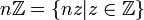, где .

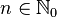• Пересечение идеалов также является идеалом (часто, особенно в коммутативной алгебре, пересечение называется наименьшим общим кратным).

23. Главный идеал кольца

Определение

Левый идеал кольца называется главным левым идеалом, если он порождён одним элементом . Аналогично определяются главные правые идеалы и главные двусторонние идеалы.

Общепринятых обозначений для главных идеалов нет. Иногда используют обозначения , , для левых, правых и двусторонних главных идеалов соответственно.

Если — коммутативное кольцо, то эти три понятия эквивалентны. В этом случае идеал, порождённый , обозначают через .

В случае ассоциативного кольца с единицей главные идеалы описываются следующим образом.

• .

• .

• .

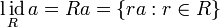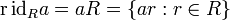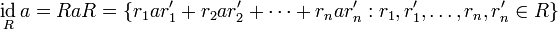Если же — ассоциативное кольцо (вообще говоря без единицы), то

• .

• .

• .

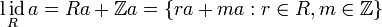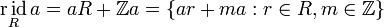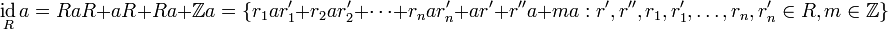Не все идеалы — главные. Рассмотрим, например, коммутативное кольцо многочленов с комплексными коэффициентами от двух переменных и . Идеал , порождённый многочленами и , (то есть идеал состоящий из многочленов, у которых свободный член равен нулю) не будет главным. Чтобы доказать это, допустим, что этот идеал порождается некоторым элементом ; тогда на него должны делиться и . Это возможно, только если — ненулевая константа. Но в только одна константа — нуль. Приходим к противоречию.

Примеры

Все евклидовы кольца являются областями главных идеалов; в них для поиска порождающего элемента данного идеала можно использовать алгоритм Евклида. Вообще, у любых двух главных идеалов коммутативного кольца есть наибольший общий делитель в смысле умножения идеалов; благодаря этому в областях главных идеалов можно вычислять (с точностью до умножения на обратимый элемент) НОД элементов и как порождающий элемент идеала .