1. Группоид

- универсальная алгебра с одной бинарной операцией. Г.- самый широкий класс таких алгебр; группы, полугруппы, квазигруппы - все это Г. специального вида. Важным понятием для Г. является понятие изотоп и и операций. Пусть на множестве Gопределены две бинарные операции, обозначаемые (Х) и (о), они изотопны, если существуют такие три взаимно однозначных отображения множества Gна себя, что для любых . Г., изотопный квазигруппе, сам является квазигруппой; Г. с единицей, изотопный группе, изоморфен этой группе. Поэтому понятием изотонии в теории групп не пользуются, для групп изотония совпадает с изоморфизмом.

Группоид с сокращением - это Г., в к-ром любое из равенств влечет (а, 6, с - элементы Г.). Каждый Г. с сокращением вложим в квазигруппу. Гомоморфный образ квазигруппы - группоид с делением, т. е. Г., в к-ром уравнения разрешимы (но не обязательно однозначно).

Множество с одной частичной (т. е. определенной не для всяких пар элементов) бинарной операцией наз. частичным группоидом. Каждый частичный подгруппоид свободного частичного Г. свободен.

Магма (группоид) в общей алгебре — алгебра, состоящая из множества М с одной бинарной операцией M × M → M. Помимо требования замкнутости множества относительно заданной на нём операции, других требований к операции и множеству не предъявляется.

Термин «магма» был предложен Бурбаки. Термин «группоид» старше, он предложен Ойстином Оре, однако этот термин также относится к другой общалгебраической структуре — теоретико-категорному группоиду, и в более современной литературе чаще используется в этом смысле.

Типы магм

Как таковые магмы обычно не изучаются; вместо этого изучаются различные типы магм, отличающиеся дополнительно вводимыми аксиомами. Обычно изучаемые типы магм включают следующие:

• квазигруппа — непустая магма, в которой всегда возможно деление;

• петля или лупа — квазигруппа с нейтральным элементом;

• полугруппа — магма с ассоциативной операцией;

• моноид — полугруппа с нейтральным элементом;

• группа — моноид с обратным элементом или, что то же, ассоциативная петля (всегда являющаяся квазигруппой);

• абелева группа — группа с коммутативной операцией.

2. Полугруппа

В математике полугруппой называют множество с заданной на нем ассоциативной бинарной операцией . Существуют разногласия по поводу того, нужно ли включать требование непустоты в определение полугруппы; отдельные авторы даже настаивают на необходимости наличия нейтрального элемента («единицы»). Однако более общепринятым является подход, согласно которому полугруппа не обязательно является непустой и не обязательно содержит нейтральный элемент. Полугруппа с нейтральным элементом называется моноидом. Следует отметить, что любую полугруппу , не содержащую нейтральный элемент, можно превратить в моноид, добавив к ней некоторый элемент и определив полученный моноид обычно обозначается как .

Примеры полугрупп

• Положительные целые числа с операцией сложения.

• Любая группа является также и полугруппой.

• Идеал кольца всегда является полугруппой относительно операции умножения.

• Множество всех отображений множества в себя с операцией суперпозиции отображений.

• Множество всех бинарных отношений на множестве с операцией умножения бинарных отношений.

• Множество всех слов над некоторым алфавитом с операцией конкатенации (присоединения)

3. ГРУППА

Гру́ппа в математике — множество элементов с определённой на нём ассоциативной бинарной операцией, унарной операцией взятия обратного элемента и выделенным нейтральным элементом, связанное некоторыми естественными свойствами — групповыми аксиомами^[⇨]. Ветвь общей алгебры занимающаяся группами, называется теорией групп.

• Наиболее известный пример группы — множество целых чисел, снабжённое операцией сложения: сумма любых двух целых также даёт целое число, число с противоположным знаком даёт обратный элемент, а роль нейтрального элемента играет нуль. Другие примеры — множество вещественных чисел с операцией сложения, множество вращений плоскости вокруг начала координат.

Непустое множество с заданной на нём бинарной операцией называется группой , если выполнены следующие аксиомы:

1. ассоциативность: ;

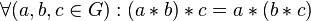2. наличие нейтрального элемента: ;

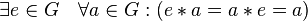3. наличие обратного элемента: