1.3. Виды и методы измерений

Процесс получения измерительной информации о физической величине может быть представлен структурной схемой [1], показанной на рис. 1.1.

Принцип измерений – это физическое явление (или эффект), положенное в основу измерений

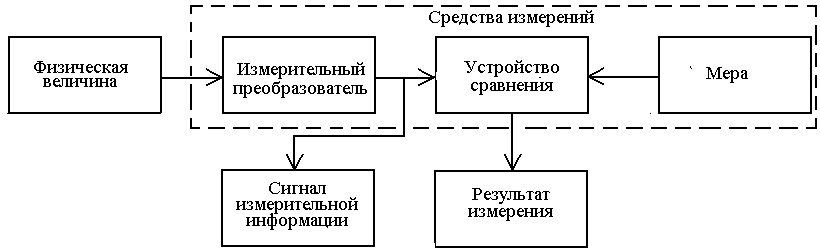
Рис. 1.1

Например: 1) применение эффекта Джозефсона для измерения электрического напряжения; 2) применение эффекта Пельтье для измерения поглощенной энергии ионизирующих излучений; 3) применение эффекта Доплера для измерения скорости и др.

Классификацию видов измерений можно проводить по различным классификационным признакам, к которым можно отнести следующие: способ нахождения численного значения физической величины, число наблюдений, характер зависимости измеряемой величины от времени, число измеряемых мгновенных значений в заданном интервале времени, условия, определяющие точность результатов, способ выражения результатов измерения.

По способу нахождения численного значения физической величины измерения подразделяются на следующие виды: прямые, косвенные, совокупные и совместные.

1) Прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно из опыта. К ним относится нахождение физической величины по шкале прибора. Примеры: измерение длины линейкой; измерение тока амперметром и т.п. В настоящее время, прямые измерения − это в основном измерения электрические. Если определяется величина неэлектрической природы, то существуют различные способы преобразования неэлектрических величин в электрические (см. главу 3). Измерение температуры ртутным градусником, давления − механическим барометром, длины − линейкой встречаются в науке и технике всё реже.

2) Косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Числовое значение искомой величины Y определяется по формуле Y = f(X₁ , X₂ …,X_n), где X₁ , X₂… X_n, – значения непосредственно измеряемых величин, а функциональная зависимость f – это какая − либо физическая закономерность, выраженная в виде формулы. Например: вычисление сопротивления R по измеренным значениям напряжения U и тока I. Другой пример – определение плотности ρ тела цилиндрической формы по результатам прямых измерений массы т, высоты h и радиуса цилиндра r, связанных с плотностью формулой .

3) Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых значения искомых величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.

Примером совокупных измерений является нахождение сопротивлений двух резисторов по результатам измерения их сопротивлений при последовательном и параллельном включении резисторов.

Для определения значений искомых величин число уравнений должно быть не меньше числа величин.

4) Совместные измерения – отличаются от совокупных тем, что производятся одновременно измерения двух или нескольких не одноименных величин для определения зависимости между ними. Числовые значения искомых величин определяют путем решения системы уравнений, связывающих значения искомых величин со значениями величин, измеренных прямым или косвенным способом. Число уравнений соответствует числу искомых величин. Примером совместных измерений может являться нахождение зависимости сопротивления резистора от температуры

R = R₀ (1 + α t),

где R – сопротивление при температуре t, R₀ – значение R при t = 0, α – температурный коэффициент. Искомыми являются R₀ и α. Измеряют два значения R: R₁ при t = t₁ и R₂ при t = t₁. Далее, решают систему двух уравнений

R₁ = R₀(1 + α t₁) ,

R₂ = R₀(1 + α t₂ ) ,

и находят искомые значения R₀ и α. Если использовать более точную зависимость R = R₀(1 + α t+ β t²), то для нахождения R₀; α и β нужны три уравнения.

Замечание. Иногда совокупные и совместные измерения считают частными случаями косвенных.

Все измерения могут производиться различными методами. Различают следующие основные методы измерений: метод непосредственной оценки и методы сравнения c мерой. Метод измерений обычно обусловлен устройством средств измерений.

Метод непосредственной оценки – это метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений. Этот метод является наиболее простым, но точность его невысока . В этом методе мера в явном виде не присутствует, она отражена в шкале. Примеры: пружинные весы, амперметр со стрелкой и шкалой и т.п.

Методы сравнения с мерой – методы измерений, в которых измеряемую величину сравнивают с величиной, воспроизводимой мерой.

П оясним сказанное следующим примером. Пусть требуется определить сопротивление R_x , сравнивая его с известным сопротивлением R₀ . Для этого соединяют их последовательно и поочерёдно измеряют напряжения U_x и U₀.

, R_x = R_{0 .}

Из последнего равенства находим неизвестное сопротивление. Ток I в данной схеме не нужно измерять.

Методы сравнения с мерой разделяются на дифференциальный метод, нулевой метод, метод замещения, метод совпадений [4]

1) Дифференциальный (разностный) метод – это метод измерений, при котором измеряемая величина сравнивается с однородной величиной (мерой), имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами. Здесь мера имеет постоянное значение Х₀, разность измеряемой величины и меры , т. е. , не равна нулю и измеряется измерительным прибором. Результат измерения Y находятся как .

То обстоятельство, что здесь измерительный прибор измеряет не всю величину Х, а только её часть , позволяет уменьшить влияние на результат измерения погрешности измерительного прибора, причем влияние погрешности измерительного прибора тем меньше, чем меньше разность . Примеры: 1) пружинные весы с маленькой платформой, на которую ставят гирю, когда масса на большой платформе превышает диапазон измерения по шкале; 2) неравновесный мост (см.параграф 2.5.2).

2) Нулевой метод измерений – это метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Изменяя величину, воспроизводимую мерой, можно довести величину  до 0. Это обстоятельство отмечается индикатором нуля. В этом случае результат измерения Y есть полученное значение меры, т. е.Y = X₀. Нулевой метод является частным случаем дифференциального при  = 0.. Примером нулевого метода является мостовой метод измерения сопротивления (см.параграф 2.5.2).

3) Метод замещения – это метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. В методе замещения, регулируя значение меры, добиваются тех же показаний прибора, что и при включении измеряемой величины. Пример применения метод замещения совместно с резонансным методом для измерения индуктивности и ёмкости представлен в параграф 2.5.2

4). Метод совпадений (метод нониуса) – это метод, в котором измеряют разность между искомой величиной и образцовой мерой, используя совпадение отметок или периодических сигналов.

Примером метода является измерение линейных размеров штангенциркулем с нониусом или стробоскоп – метка на вращающемся теле освещается вспышками лампы и кажется неподвижной, когда частота вспышек равна (или кратна) частоте вращения

Различают также контактный и бесконтактный методы измерений.

Контактный метод – это метод измерений, основанный на том, что чувствительный элемент прибора приводится в контакт с объектом измерения (например, измерение температуры тела термометром).

Бесконтактный метод – это метод измерений, основанный на том, что чувствительный элемент средства измерений не приводится в контакт с объектом измерения (например, измерение температуры в доменной печи пирометром).