1.5.1. Рассмотрим последовательность силового расчета для кривошипно-ползунного механизма.

К звеньям 3 и 4 двухповодковой группы (см. рис. ПI.г.), выделенной в заданном рабочем положении механизма, прикладываются по направлениям их действия все силы и реакции отсоединенных звеньев. В начале рассматривается равновесие шатуна из условия:

В результате решения этого уравнения определяется – тангенциальная составляющая реакция в паре “ ”. Составим уравнение сил, действующих на звенья группы 3 – 4 из условия

В этом уравнении реакции и , известны по направлениям. Определим графоаналитическим способом, то есть построением плана сил все неизвестные составляющие. План сил двухповодковой группы (3 - 4) Ассура показан на рис. П1. Д., выполненный в масштабе.

Построение плана сил начинаем с вектора тангенциальной составляющей реакции в кинематической паре ” ”. Приняв масштаб из точки 2 откладываем отрезок в направлении перпендикулярном звену в заданном положении. Длина отрезка (2 - 3) выбирается из расчета , мм. Значение силы | | определим из уравнения моментов сил (23). Далее из точки 3 откладываем в принятом масштабе отрезок (3 - 4), соответствующий величине силы инерции в принятом масштабе . Отрезок , мм.

Исходя из условия равновесия сил системы тел векторный многоугольник сил должен быть замкнут. Для этого из точки 2 проведем линию параллельно до пересечения с линией, проведенной из точки 5 перпендикулярно оси (x - x) – траектории движения ползуна. Точку пересечения 1 соединяем с точкой 3 плана сил и замыкаем векторный многоугольник. Отрезок соответствующий полной реакции | | в отсоединенной кинематической паре “ ” на шатуне. Отрезок соответствующей реакции | | в кинематической паре “ ” двухповодковой группы Ассура (ползун-шатун). С целью упрощения построения плана сил не учтены силы тяжести звеньев шатуна и ползуна . Зная масштаб сил , измерив на плане сил (рис. П1. д.) отрезки векторов сил | | и | |, получим значение этих сил по величине или по модулю:

| =

Аналогично определяем остальные составляющие силы. Так, полная реакция от силы давления в паре ” ” на кривошип | | определяется, как геометрическая сумма ее составляющих:

Из плана сил имеем

Если точка приложения реакции не совпадает с парой “ ”, то есть когда центр масс ползуна находится на каком-то расстоянии от точки “ ”, тогда составляют уравнение равновесия звена 4 /ползуна/ из условия:

В нашем примере все силы звена проходят через точку “ ” и поэтому плечо реакции .

1.5.2. Силовой расчет входного звена.(кривошипа)

Входное или начальное звено-кривошип должно находиться в равновесии под воздействием силы давления в паре “ ”.

Для этого необходимо определить уравновешивающую силу или момент, а также реакции в паре кривошип-стойка. Под урав­новешивающими силами или моментами подразумевают те внешние силы и моменты, которые обеспечивают заданное движение механизма. Ес­ли движение передается от привода через муфту, то можно записать условие равновесия кривошипа в виде:

Отсюда находим значение уравновешивающего момента:

Где - масштаб плана положения кривошипа (см. рис. П1.е).

Реакция на стойке может быть определена из плана сил, действующих на кривошип и стойку. Исходя из условия равновесия запишем: . Отсюда следует:

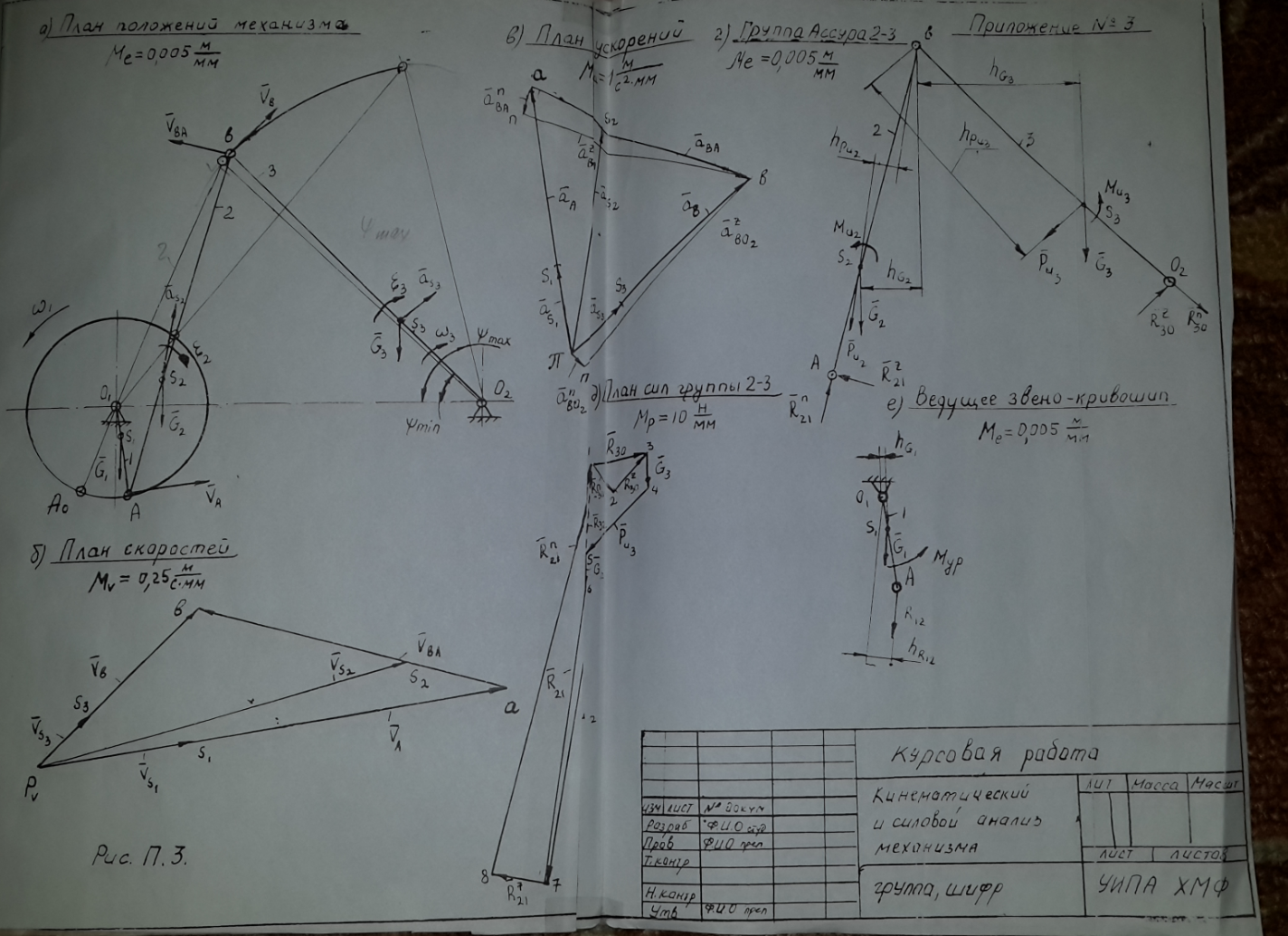
Силовой расчет кривошипно-коромыслового механизма производится графоаналитическим способом в такой же последовательности с учетом его особенностей в части выходного звена-коромысла. План сил для двухповодковой группы Ассура кривошипно-коромыслового механизма приводится на рис. ПЗ.д. (см. приложение №3). Условие равновесия кривошипа для этого механизма показано на плане положения входного—ведущего звена (см. рис. ПЗ. е.) .

В приложении №3 приведены: план положений кривошипно-коромыслового механизма (рис. ПЗ. а.); план скоростей (рис. ПЗ. б.); план ускорений (рис. ПЗ. в.); двухповодковая группа Ассура (шатун 2- ко­ромысло 3, см. рис. ПЗ. г.); план сил группы звеньев 2-3 (см.рис. ПЗ. д.); план положения ведущего звена-кривошипа (рис. ПЗ. е.). Все построения выполнены в соответствующих масштабах.

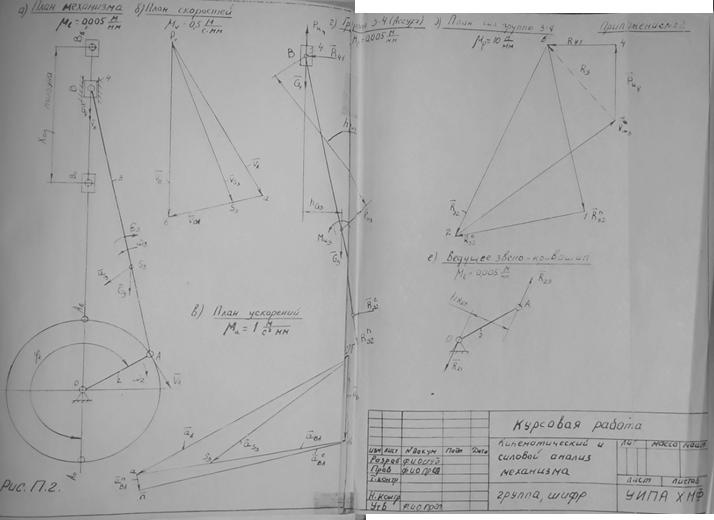
В приложении №2 приведен в качестве примера кинематический и силовой анализ кривошипно-ползунного механизма с вертикальным расположением оси перемещения выходного звена-поршня. На рис.П2.а. показан план положений механизма на рабочем ходу и крайние положения кривошипа определяющие ход ползуна-поршня при его перемещении в направлении оси (x - x). На рис.П2.б. показан план скоростей в заданном положении на рабочем ходу. На рис. П2.в. по­казан план ускорений. На рис. П2. г. показана двухповодковая груп­па Ассура (звеньев 3-4; шатун -ползун), выполненная в масштабе плана положений механизма. К ней приложены действующие силы и реакции в отсоединенных кинематических парах "А" и "В". На рис. ПЗ. д. приведен план cил группы звеньев 3-4, выполненный в масштабе . На рис. П2. е. показано ведущее звено-кривошип с при ложенными к нему силами и реакциями. Все построения выполнены в соответствующих масштабах.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

1. Артобалевский И.И. Теории механизмов и машин.- Наука, 1985 г. 636 с.

2. Кореняко A.C. и др. Теория механизмов и машин. - Киев:

Высшая школа, 1976 г. - 443 с.

3. Машнев М .Н. и др. Теория механизмов и машин и детали машин. -JI.: Машиностроение, I960. -511 с.