24 Билет

1) Электр Қозғаушы Күш – электр тізбегіне жалғанған, табиғаты электрстатикалық емес энергия көзі. Тек қана электрстатик. күштер тұйық тізбекпен тұрақты токтың үздіксіз жүруін қамтамасыз ете алмайды. Өйткені бұл күштердің тұйық контур бойымен зарядты қозғалтуы үшін жұмсайтын жұмысы нөлге тең, ал ток жүрген кезде әдетте энергия шығыны болады. Сондықтан тұйық контурмен үздіксіз ток жүруі үшін электр тізбегінен тыс басқа бір энергия көзі болу керек. Бұл энергия көзі энергияны сырттан ала отырып, оны зарядтардың қозғалыс энергиясына айналдырады да, қосымша электр өрісін (Е) тудырады. Мұндай қосымша электр өрісі күшінің тұйық контур бойымен істейтін жұмысы нөлге тең болмайды: . Е' шамасы Э. қ. к. деп аталады және оның шамасы бірлік зарядты қозғалтуға кететін электрстатик. емес күштердің жұмысына тең. Потенциал сияқты Э. қ. к-тің де өлшеу бірлігі – вольт (в). Электролиттердегі иондардың диффузиясы, контур арқылы өткен магнит ағынының өзгеруі (эл.-магн. индукция), т.б. Э. қ. к-ін тудырады. 

2) Бірізді жалғанған r, L және C элементтерден тұратын электр тізбегі арқылы ( 20-сурет) синусоидалы ток i=I_msin t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= u_r+u_L+u_C. Онда тізбек күйінің теңдеуі: u= ri+ L + = rI_msin t+I_m Lcos t - 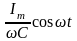немесе

u=rI_msin t+I_m Lsin( t+90^o)+ =U_mrsin t+U_mLsin( t++90^o) +U_mcsin( t - 90^o).

Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I ,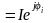

U_r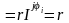 I, U_L I , U_C= I , U= , j=e^j90˚, -j=e^-j90˚

20 Сурет

25 Билет

1) Магниттік ағын, магниттік индукция ағыны — белгілі бір бет арқылы өтетін магниттік индукция векторының (В) ағыны (Ф). Егер dS шағын аудандағы В магнит индукция векторы тұрақты шама деп есептелсе, онда осы аудан арқылы өтетін Магниттік ағын (Ф) аудан мөлшері мен В векторының осы аудан нормалына түсірілген проекциясының (Вn) көбейтіндісіне тең: dФ=ВndS. Шектелген бет (S) арқылы өтетін Магниттік ағын (Ф) төмендегі интеграл бойынша анықталады: Ф= Тұйықталған бет үшін бұл интеграл нөлге тең, бұл жағдай магнит өрісініңсоленоидтық сипатын, яғни табиғатта магнит зарядтардың — магнит өрісі көздерінің (магнит өрісін электр токтары туғызады) жоқ екендігін көрсетеді. Бірліктердің халықаралық жүйесіндегі (СИ) өлшем бірлігі —

вебер (Вб)

Бірліктердің СГС жүйесінде —

максвелл (Мкс);

1 Вб=108 Мкс.

2)

Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбегін синусоидалы кернеуге u=U_msinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша:

, немесе i=(U_m/r)sinωt+(U_m/ωL) sin(ωt-90˚)+ωCU_m sin(ωt+90˚).

Комплекстік әрекеттік мәндерге көшейік:

I=Ie^jφ, I_a= I_ae^j0, I_L=I_Le^-j90˚ , I_C=I_Ce^j90˚ , мұндағы I_a=U/r, I_L=U/ωL,

I_C=UωC – токтардың модульдері, ал U=U_m/ . Алынған теңдеуден активті кедергідегі токтың фаза бойынша кернеумен бірдей болатынын көреміз. Ток индуктивті элементте фаза бойынша 90˚ артта қалады, ал ток сыйымдылық элементтегі кернеуден фаза бойынша 90˚ озады. Кернеу мен токтардың векторларының өзара орналасуы 26-суреттегі векторлық диаграммада көрсетілген. Индуктивті ток I_L пен сыйымдылық токтың I_C фазалары қарама-қарсы болғандықтан олар бір бірінен алынады.