
- •1 Билет
- •2 Билет
- •3 Билет
- •4 Билет
- •5 Билет
- •6 Билет
- •Д) Параллель жалғанған қоректендіргіштерді бір балама қоректендіргішпен айырбастауға (түрлендіруге) болады (5-сурет) .
- •7 Билет
- •8 Билет
- •9 Билет
- •10 Билет
- •11 Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •16 Билет
- •17 Билет
- •18 Билет
- •19 Билет
- •20 Билет
- •21 Билет
- •22 Билет
- •23 Билет
- •24 Билет
- •20 Сурет
- •25 Билет
- •26 Билет
- •27 Билет
- •28 Билет
- •29 Билет
- •30 Билет
- •31 Билет
- •32 Билет
- •33 Билет
- •34 Билет
11 Билет
1)
14-сурет |
Лездік қуат тұрақты құраушыдан және екі еселенген жиілікпен өзгеретін айнымалы құраушыдан тұрады ( 14-сурет). Оның таңбасы әр уақытта оң, яғни электр энергиясы тұрақты түрде басқа түрлі энергияға түрленеді. Период ішіндегі орташа қуатты активті қуат деп атаймыз: P=
|
2 )
Сұлбалардағы түйіндердің
потенциалдарын белгісіз ретінде
қабылдап, электр тізбектерін есептеу
тәсілін түйіндік
потенциалдар тәсілі деп атайды.Айталық,
сұлбада n-түйін болсын. Сұлбаның кез-келген
бір нүктесін ойша жермен қосамыз, яғни
оның потенциалын нөлге тең деп аламыз.Соның
нәтижесінде белгісіздер саны
n-1-ге дейін азаяды. Бұл
тәсіл бойынша теңдеулер Кирхгофтың
бірінші заңы бойынша түйінде түйіскен
токтарға арнап құрылады.
Токтарды түйіндердің потенциалдары
арқылы Ом заңы бойынша өрнектеуге
болады. Нәтижесінде теңдеулер жүйесі
мынадай түрде жазылады:
)
Сұлбалардағы түйіндердің
потенциалдарын белгісіз ретінде
қабылдап, электр тізбектерін есептеу
тәсілін түйіндік
потенциалдар тәсілі деп атайды.Айталық,
сұлбада n-түйін болсын. Сұлбаның кез-келген
бір нүктесін ойша жермен қосамыз, яғни
оның потенциалын нөлге тең деп аламыз.Соның
нәтижесінде белгісіздер саны
n-1-ге дейін азаяды. Бұл
тәсіл бойынша теңдеулер Кирхгофтың
бірінші заңы бойынша түйінде түйіскен
токтарға арнап құрылады.
Токтарды түйіндердің потенциалдары
арқылы Ом заңы бойынша өрнектеуге
болады. Нәтижесінде теңдеулер жүйесі
мынадай түрде жазылады:
φ1G11 + φ2G12 + φ3G13= I11
φ1G21 + φ2G22 + φ3G23= I22
φ1G31 + φ2G32 + φ3G33= I33
φ1, φ2, φ3- бірінші, екінші және үшінші түйіндердің потенциалдары; G11, G22, G33-- бірінші, екінші және үшінші түйіндерде түйіскен тармақтардың өткізгіштердің қосындысы; Gkm- k мен m түйіндерді байланыстыратын тармақтың өткізгіштігі, “минус” таңбасымен алынады; I11, I22, I33- түйіндердің түйіндік токтары. Белгілі бір түйіннің түйіндік тогы сол түйінмен байланысқан тармақтардағы э.қ.к.-терді сол тармақтардың кедергілеріне бөлу арқылы табылған токтардың алгебралық қосындысына тең. Э.қ.к.-тері түйінге бағытталған тармақтардың токтары «плюс» таңбасымен алынады, ал керісінше жағдайда «минус»таңбасы алынады.
12 Билет
1) Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА].
2) Электр сұлбаларының топологиялық элементтері. Тармақ деп элементтері бір-бірімен бірізді жалғанған, бойымен бір ғана тоқ жүретін тізбек бөлігін айтамыз. Түйін деп кем дегенде үш тармақтың түйіскен нүктесін айтады. Контур деп бірнеше тармақ арқылы өтетін тізбектің тұйық бөлігін айтады.
13 Билет
1)
Лездік реактивті қуаттың амплитудасын
(UIsin
) реактивті қуат
Qp=
UIsin
деп атайды. Өлшем бірлігі- вольтампер
реактивтік [ВАр]. Qp=
QL –
QC=
xLI2
– xCI2=
ULI –
UC I
=Up I.
Кедергілер үшбұрышының қабырғаларын
I2
көбейтсек, онда қуаттар үшбұрышын
аламыз. Оның бір катеті активті қуатқа
P, екінші катеті реактивті қуатқа Qp
, ал гипотенузасы толық қуатқа S сәйкес
келеді. Бұл үшбұрыштан толық қуат: S= ,
φ= arctg Qp/
P, немесе P= Scos
,
Qp =
Ssin
.
,
φ= arctg Qp/
P, немесе P= Scos
,
Qp =
Ssin
.
2) Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды. Мысалы, 7-суреттегі тізбектің тармақтарындағы токтарды табайық. Ол үшін алдымен Uаб кернеуін табамыз. Тізбектің «б » түйінінің потенциалын нөлге тең деп аламыз. Сонда Uаб=φа – φб = φа – 0 = φа.
Тізбектің «а » түйіні үшін: I1 + I2 +I3 + I4=0,
мұндағы I1= (E1 - Uаб)/R1=(E1-φа)/R1,
I2= - Uаб . R2= -φа . R2, I3= (-E3 - Uаб).R 3=(-E3-φа).R3, I4= -φа . R4.
Токтардың өрнектерін теңдеуге қоямыз да , φа табамыз:
φа(g1+g2+g3+g4)= E1g1 – E3g3,
φа=(E1g1 – E3g6)/ (g1+g2+g3+g4).
Табылған φа мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Табылған φа мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Жалпы жағдайда Uаб =∑ Eкgк /∑gк.

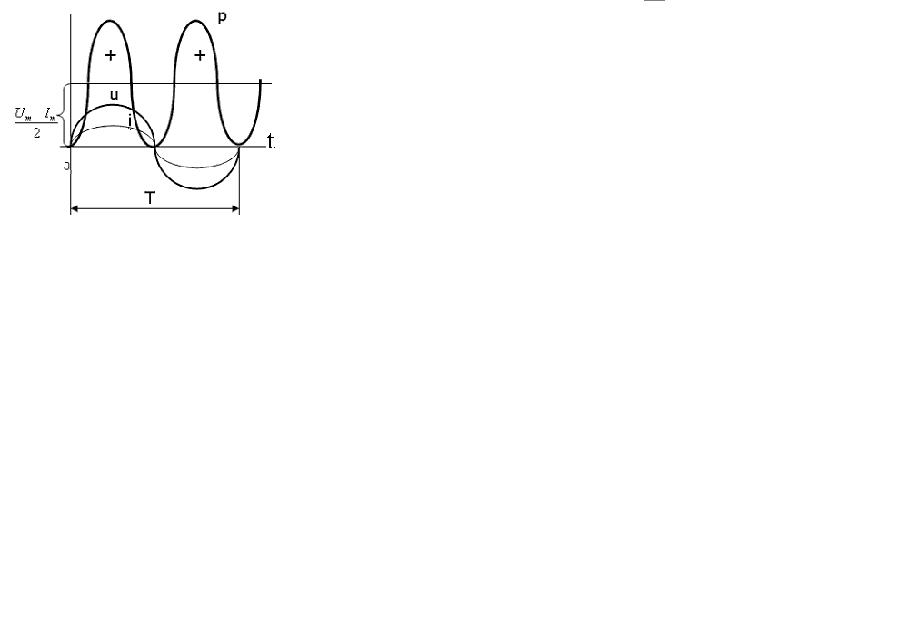
 ,
немесе P=UI= =I2 r
=
,
немесе P=UI= =I2 r
=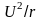 .
Активті қуаттың өлшем бірлігі ретінде
Ватт ( Вт) қабылданған.
.
Активті қуаттың өлшем бірлігі ретінде
Ватт ( Вт) қабылданған.