5 Оцінка сталості системи з оптимальними настройками
Оцінка сталості замкнутої системи виконується за допомогою критерію Найквіста-Михайлова. Для цього на комплексній площині необхідно побудувати АФХ розімкнутої системи (годограф Найквіста), яка містить в собі об’єкт та регулятор із знайденими оптимальними настройками.
Враховуючи послідовну схему з’єднання регулятора та об’єкта, частотна передаточна функція розімкнутої системи регулювання представляє добуток передаточної функції регулятора та об’єкта:
(5.1)
Модуль
вектора АФХ розімкнутої системи
визначається як добуток
і
,
а аргумент – як сума
і
:
(5.2)
(5.3)
Для кожного заданого значення частоти визначають модуль і аргумент об’єкта і регулятора, після чого розраховують модуль і аргумент АФХ розімкнутої системи. З’єднавши кінці отриманих таким чином векторів плавною кривою, отримують АФХ розімкнутої системи (рис. 5.1).
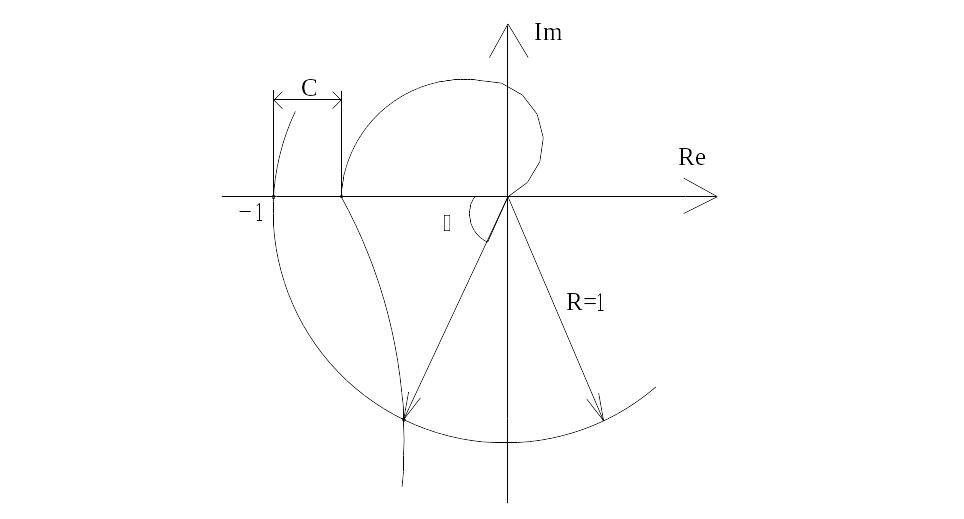
Рис. 5.1 Годограф Найквіста з зазначенням розрахунку запасу стійкості
Якщо АФХ не охоплює точку з координатами (–1, j0), згідно з критерієм Найквіста-Михайлова, система стала.
Запас сталості за модулем визначається як відстань від точки тину АФХ з від’ємною піввіссю до початку координат. Запас сталості за фазою визначається як кут між від’ємною піввіссю, та променем, проведеним з початку координат через точку пересічення АФХ і кола радіусом 1 з центром в початку координат.
Вважають, що система стала, якщо виконуються наступні умови:
,
(5.4)
(5.5)
Якщо система за будь-яким показником не входить у зазначений діапазон, рекомендується удосконалити її. Для цього необхідно ввести корегуючу ланку у головний контур, що дозволить збільшити сталість системи.
6 Оцінка якості замкнутої системи
Для оцінки якості замкнутої системи регулювання за допомогою прямих критеріїв необхідно побудувати процес в замкнутій системі регулювання. В разі відомих передаточних функцій об’єкта і регулятора і місця прикладання зовнішньої дії можливо виконати розрахунок перехідної характеристики в замкнутій системи регулювання різними методами:
пряме вирішення диференційного рівняння;
застосування методу зворотного перетворення Лапласа;
за дійсною частотною характеристикою (ДЧХ).
При вирішенні диференційного рівняння необхідно задати весь набір початкових умов та визначити усі корені характеристичного рівняння замкнутої системи регулювання. Додатково, необхідно вказати знаки змінних та їх похідних при нульових початкових умовах. На базі встановлених початкових умов визначаються всі постійні інтегрування. Корені характеристичного рівняння використовуються у розрахунку в експоненційних та всіх періодичних складових рішення диференційного рівняння.
Метод зворотного перетворення Лапласа потребує визначення всіх початкових умов. Крім того, передаточну функцію АСР необхідно розкласти на добуток елементарних функцій, що відповідають типовим ланкам. За таблицею зворотних перетворень Лапласа знайти рішення для цих складових та побудувати результуючий перехідний процес для АСР у цілому.
У курсової роботі розрахунок перехідної характеристики виконується по дійсній частотній характеристиці замкнутої системи Р( ).Взаємний зв’язок перехідної характеристики і дійсної частотної характеристики:
(6.1)
Інтегрувати рівняння (6.1) досить важко, тому використовується приблизне рішення задачі за методом трапецій та трикутників [4]. Вихідною інформацією в такому разі є дійсна частотна характеристика замкнутої системи.
Дійсна частотна характеристика замкнутої системи може бути побудована на основі АФХ розімкнутої системи. Частотна передаточна функція замкнутої системи має вигляд:
(6.2)
Згідно з (6.2) знаменник частотної передаточної функції замкнутої системи є збільшена на одиницю частотна передаточна функція розімкнутої системи. Таким чином, якщо піввісь ординат перенести ліворуч на одиницю, АФХ розімкнутої системи перетворюється на АФХ знаменника частотної передаточної функції замкнутої системи. Після цього з нового початку координат в точки АФХ з відомими значеннями ( ) будують вектори и вимірюють їх модулі і аргументи (рис. 6.1).
Рис. 6.1 Визначення модуля та аргументу вектору знаменника передаточної функції замкнутої системи (зс)
Модуль вектора АФХ замкнутої системи визначають як частку від ділення модуля вектора АФХ розімкнутої системи на модуль АФХ знаменника частотної передаточної функції замкнутої системи при тій самій частоті:
(6.3)
Аргумент
вектора АФХ замкнутої системи визначається
як різниця між аргументами АФХ розімкнутої
системи(
)
і АФХ знаменника частотної передаточної
функції замкнутої системи (
)
при однакових частотах:
(6.4)
Ордината дійсної частотної характеристики при відповідних частотах визначається як добуток модуля АФХ замкнутої системи на косинус її аргументу:
(6.5)
Отримані, таким чином, координати точок ДЧХ замкнутої системи, наносять у координатах: частота ( ) – дійсне значення АФХ замкнутої системи (Р( )). З’єднавши отримані точки плавною кривою, отримують графік дійсної частотної характеристики замкнутої системи (рис.6.2).
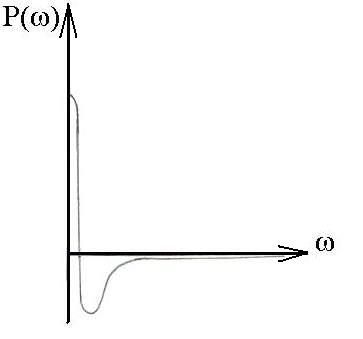
Рис. 6.2 Дійсна частотна характеристика замкнутої системи
Крива ДЧХ замінюється послідовністю горизонтальних і похилих відрізків [6]. Площину обмежену кривою ДЧХ і осями координат замінюють сукупністю трапецій і трикутників, дві з сторін яких лежать на півосях координат. Для кожної трапеції або трикутника за допомогою таблиці h-функції (див. додатки) будують сепаратний перехідний процес. В h-функції відображена реакція системи на одиничну стрибкоподібну вхідну дію, якщо її ДЧХ відповідає одиничній трапеції (рис. 6.3).
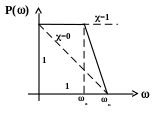
Рис. 6.3 Одинична трапеція ті її характеристики
Одинична трапеція - це трапеція, основа та висота дорівнює дорівнюють одиниці. Частоту у точці ізлому позначимо через а ; частоту у точці, що відповідає кінцевій точці більшої основи трапеції позначимо через к (частота зрізу). Показник нахилу відображає відношення частот:
(6.6)
Показник
нахилу знаходиться у межах
.При
отримуємо трикутник,
– отримуємо квадрат. Для кожної з
виділених трапецій (трикутників)
необхідно визначити показник нахилу.
За цим показником визначається перехідний
процес за таблицею h-функцій.
Усі знайдені трапеції переміщують за вертикаллю вгору або вниз до тих пір, поки більша основа трапеції не ляже на ось абсцис. Знак відхилення кожного з сепаратних процесів визначається в залежності від розташування відповідної трапеції відносно півосі абсцис. Трапеції, які розташовані понад піввіссю абсцис – позитивні, а ті що під нею – негативні.
З
метою приведення табличних перехідних
функцій в разі коли ДЧХ відповідає
неодиничній трапеції використовують
відповідне масштабування. При цьому
ординати кожної h-функції (
)
множаться на висоту (
)
відповідної трапеції з урахуванням її
знаку:
(6.7)
Абсциса
трапеції розраховується як відношення
табличного значення часу (
)
до її частоти зрізу (
):
(6.8)
По завершенню масштабування отримані таким чином сепаратні перехідні процеси підсумовуються графічним методом (рис. 6.4). В результаті отримують перехідну функцію в синтезованій системі регулювання. З метою отримання перехідної характеристики синтезованої системи регулювання в разі нанесення на її вхід завданої дії, кожна ордината перехідної функції помножується на величину вхідної дії.
Рис. 6.4 Визначення перехідного процесу за методом трапецій
За допомогою отриманого перехідного процесу у замкнутій системі визначають прямі показники якості (час регулювання – tp, максимальне динамічне відхилення – удин) і зрівнюють їх із завданими (рис. 6.5) та роблять висновок про працездатність системи та можливість її застосування.
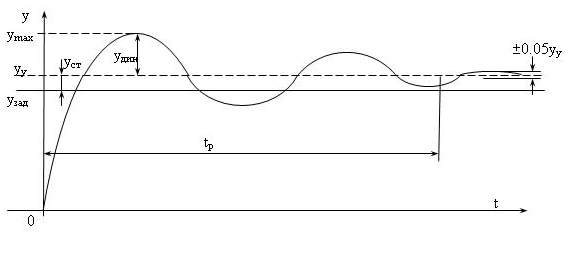
Рис. 2.24 – Оцінка якості по кривій перехідного процесу
СПИСОК ЛІТЕРАТУРИ
Глинков Г.М., Маковский В.А., Лотман С.Л. Проектирование систем контроля и автоматического регулирования металургических процессов.-М.: Металургия, 1970.
КопеловичА.П. Инженерные методы расчета при выборе автоматических регуляторов.- М.: Металургиздат, 1960.
Климовицкий М.Д., КопеловичА.П. Автоматический контроль и регулирование в черной металургии. Справочник.-М: Металургия, 1967.
Прусенко В.С. Одноконтурные пневматические системы автоматического регулирования тепловых процессов.-М.: Госэнергоиздат, 1963.
Широкий Д.К., Куреленко О.Д. Оптимальні настройки промислових систем регулювання. – Київ: Вища школа, 1975. – 264 с.
Теория автоматического регулирования. Книга 1. Математическое описание, анализ устойчивости и качества систем автоматического регулирования. Под редакцией Солодовникова В.В. – М.: Машиностроение, 1967. – 768 с.
Теория автоматического регулирования. Книга 2. Анализ и синтез линейных непрерывных и дискретных систем автоматического регулирования. Под редакцией Солодовникова В.В. – М.: Машиностроение, 1967. – 680 с.
Джон М. Смит. Математическое и цифровое моделирование для инженеров и исследователей. – М.: Машиностроение, 1980. – 272 с.
ДОДАТКИ
Таблиця h-функцій для нормованої трапецеїдальної дійсної частотної функції
х |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0,138 |
0,165 |
0,176 |
0,184 |
0,192 |
0,199 |
0,207 |
1 |
0,31 |
0,326 |
0,34 |
0,356 |
0,371 |
0,386 |
0,401 |
1,5 |
0,449 |
0,469 |
0,494 |
0,516 |
0,538 |
0,56 |
0,594 |
2 |
0,572 |
0,597 |
0,628 |
0,665 |
0,683 |
0,709 |
0,681 |
2,5 |
0,674 |
0,707 |
0,739 |
0,771 |
0,802 |
0,833 |
0,862 |
3 |
0,755 |
0,79 |
0,828 |
0,863 |
0,896 |
0,928 |
0,958 |
3,5 |
0,783 |
0,853 |
0,892 |
0,928 |
0,963 |
0,994 |
1,024 |
4 |
0,857 |
0,896 |
0,938 |
0,974 |
1,008 |
1,039 |
1,06 |
4,5 |
0,883 |
0,923 |
0,96 |
0,997 |
1,029 |
1,057 |
1,08 |
5 |
0,896 |
0,936 |
0,978 |
1,012 |
1,042 |
1,067 |
1,087 |
5,5 |
0,9 |
0,94 |
0,986 |
1,019 |
1,046 |
1,067 |
1,083 |
6 |
0,904 |
0,942 |
0,982 |
1,013 |
1,037 |
1,054 |
1,065 |
6,5 |
0,904 |
0,943 |
0,98 |
1,009 |
1,03 |
1,043 |
1,05 |
7 |
0,904 |
0,944 |
0,979 |
1,006 |
1,024 |
1,035 |
1,037 |
7,5 |
0,907 |
0,945 |
0,98 |
1,006 |
1,019 |
1,025 |
1,025 |
8 |
0,91 |
0,951 |
0,985 |
1,008 |
1,02 |
1,024 |
1,021 |
8,5 |
0,918 |
0,956 |
0,989 |
1,01 |
1,021 |
1,022 |
1,018 |
9 |
0,924 |
0,965 |
0,997 |
1,016 |
1,025 |
1,025 |
1,018 |
9,5 |
0,932 |
0,972 |
1,004 |
1,022 |
1,029 |
1,027 |
1,019 |
10 |
0,939 |
0,978 |
1,009 |
1,025 |
1,031 |
1,027 |
1,019 |
10,5 |
0,946 |
0,985 |
1,013 |
1,028 |
1,033 |
1,028 |
1,017 |
11 |
0,947 |
0,988 |
1,015 |
1,029 |
1,031 |
1,025 |
1,014 |
11,5 |
0,949 |
0,988 |
1,016 |
1,027 |
1,028 |
1,021 |
1,01 |
12 |
0,95 |
0,988 |
1,015 |
1,025 |
1,024 |
1,015 |
1,004 |
12,5 |
0,95 |
0,989 |
1,013 |
1,022 |
1,019 |
1,01 |
0,999 |
13 |
0,95 |
0,989 |
1,012 |
1,019 |
1,015 |
1,005 |
0,994 |
13,5 |
0,95 |
0,99 |
1,011 |
1,017 |
1,011 |
1 |
0,99 |
14 |
0,952 |
0,989 |
1,011 |
1,016 |
1,009 |
0,997 |
0,988 |
14,5 |
0,954 |
0,99 |
1,012 |
1,015 |
1,008 |
0,996 |
0,987 |
15 |
0,956 |
0,993 |
1,012 |
1,014 |
1,007 |
0,995 |
0,988 |
15,5 |
0,959 |
0,995 |
1,014 |
1,014 |
1,006 |
0,995 |
0,989 |
16 |
0,961 |
0,997 |
1,015 |
1,014 |
1,006 |
0,995 |
0,991 |
16,5 |
0,964 |
0,999 |
1,016 |
1,014 |
1,005 |
0,995 |
0,993 |
17 |
0,965 |
1,001 |
1,016 |
1,013 |
1,005 |
0,995 |
0,994 |
17,5 |
0,966 |
1,002 |
1,015 |
1,012 |
1,003 |
0,995 |
0,994 |
18 |
0,966 |
1,002 |
1,015 |
1,011 |
1,002 |
0,995 |
0,995 |
18,5 |
0,966 |
1,001 |
1,015 |
1,009 |
1,001 |
0,994 |
0,995 |
19 |
0,967 |
1 |
1,015 |
1,008 |
0,998 |
0,992 |
0,995 |
19,5 |
0,967 |
1 |
1,014 |
1,006 |
0,996 |
0,991 |
0,995 |
20 |
0,967 |
1 |
1,013 |
1,005 |
0,995 |
0,991 |
0,995 |
20,5 |
0,968 |
1,002 |
1,012 |
1,004 |
0,994 |
0,991 |
0,996 |
21 |
0,968 |
1,002 |
1,011 |
1,003 |
0,994 |
0,992 |
0,997 |
21,5 |
0,969 |
1,002 |
1,011 |
1,003 |
0,995 |
0,992 |
0,999 |
22 |
0,971 |
1,002 |
1,011 |
1,002 |
0,995 |
0,993 |
1 |
22,5 |
0,973 |
1,002 |
1,011 |
1,002 |
0,996 |
0,995 |
1,002 |
23 |
0,974 |
1,005 |
1,011 |
1,002 |
0,996 |
0,996 |
1,004 |
23,5 |
0,975 |
1,005 |
1,01 |
1,002 |
0,996 |
0,998 |
1,004 |
24 |
0,975 |
1,005 |
1,01 |
1,001 |
0,996 |
0,999 |
1,005 |
24,5 |
0,975 |
1,005 |
1,009 |
1 |
0,996 |
0,999 |
1,005 |
25 |
0,975 |
1,005 |
1,008 |
1 |
0,995 |
0,999 |
1,005 |
25,5 |
0,975 |
1,005 |
1,008 |
0,999 |
0,995 |
0,999 |
1,004 |
26 |
0,975 |
1,005 |
1,007 |
0,999 |
0,995 |
0,999 |
1,004 |
Продовження таблиці
х |
0,35 |
0,4 |
0,45 |
0,5 |
0,55 |
0,6 |
0,65 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0,215 |
0,223 |
0,231 |
0,24 |
0,248 |
0,255 |
0,259 |
1 |
0,417 |
0,432 |
0,447 |
0,461 |
0,476 |
0,49 |
0,505 |
1,5 |
0,603 |
0,616 |
0,646 |
0,665 |
0,685 |
0,706 |
0,722 |
2 |
0,761 |
0,786 |
0,81 |
0,833 |
0,856 |
0,878 |
0,899 |
2,5 |
0,891 |
0,917 |
0,943 |
0,967 |
0,985 |
1,01 |
1,03 |
3 |
0,987 |
1,013 |
1,038 |
1,061 |
1,082 |
1,1 |
1,117 |
3,5 |
1,05 |
1,095 |
1,115 |
1,115 |
1,132 |
1,145 |
1,158 |
4 |
1,09 |
1,107 |
1,124 |
1,142 |
1,152 |
1,158 |
1,159 |
4,5 |
1,1 |
1,115 |
1,129 |
1,138 |
1,134 |
1,134 |
1,138 |
5 |
1,103 |
1,112 |
1,117 |
1,118 |
1,115 |
1,107 |
1,098 |
5,5 |
1,093 |
1,095 |
1,097 |
1,092 |
1,083 |
1,07 |
1,05 |
6 |
1,07 |
1,068 |
1,062 |
1,051 |
1,037 |
1,021 |
1,003 |
6,5 |
1,049 |
1,043 |
1,033 |
1,018 |
1,001 |
0,982 |
0,946 |
7 |
1,033 |
1,023 |
1,009 |
0,993 |
0,975 |
0,957 |
0,941 |
7,5 |
1,017 |
1,005 |
0,989 |
0,974 |
0,958 |
0,944 |
0,926 |
8 |
1,012 |
0,995 |
0,981 |
0,966 |
0,951 |
0,941 |
0,935 |
8,5 |
1,007 |
0,992 |
0,977 |
0,996 |
0,949 |
0,944 |
0,948 |
9 |
1,006 |
0,992 |
0,978 |
0,97 |
0,96 |
0,961 |
0,966 |
9,5 |
1,006 |
0,993 |
0,982 |
0,975 |
0,972 |
0,98 |
0,987 |
10 |
1,006 |
0,993 |
0,987 |
0,982 |
0,985 |
0,933 |
1,006 |
10,5 |
1,005 |
0,993 |
0,991 |
0,987 |
0,996 |
1,007 |
1,017 |
11 |
1,002 |
1,993 |
0,991 |
0,993 |
1,002 |
1,014 |
1,027 |
11,5 |
0,999 |
0,991 |
0,989 |
0,997 |
1,006 |
1,017 |
1,029 |
12 |
0,994 |
0,988 |
0,987 |
0,997 |
1,006 |
1,019 |
1,026 |
12,5 |
0,99 |
0,986 |
0,986 |
0,997 |
1,006 |
1,018 |
1,019 |
13 |
0,986 |
0,985 |
0,987 |
0,997 |
1,006 |
1,014 |
1,012 |
13,5 |
0,983 |
0,984 |
0,988 |
0,988 |
1,006 |
1,01 |
1,005 |
14 |
0,983 |
0,985 |
0,991 |
1 |
1,006 |
1,008 |
0,999 |
14,5 |
0,985 |
0,988 |
0,996 |
1,002 |
1,006 |
1,005 |
0,994 |
15 |
0,987 |
0,991 |
1 |
1,005 |
1,007 |
1,002 |
0,993 |
15,5 |
0,988 |
0,996 |
1,004 |
1,008 |
1,007 |
1,001 |
0,993 |
16 |
0,992 |
0,998 |
1,007 |
1,011 |
1,008 |
1 |
0,994 |
16,5 |
0,995 |
1,002 |
1,009 |
1,011 |
1,008 |
1,001 |
0,996 |
17 |
0,997 |
1,005 |
1,01 |
1,012 |
1,007 |
0,999 |
0,997 |
17,5 |
0,998 |
1,006 |
1,01 |
1,009 |
1,005 |
0,997 |
0,998 |
18 |
1,001 |
1,008 |
1,01 |
1,008 |
1,002 |
0,997 |
0,998 |
18,5 |
1,001 |
1,007 |
1,009 |
1,006 |
0,999 |
0,995 |
0,998 |
19 |
1,001 |
1,006 |
1,006 |
1,001 |
0,995 |
0,993 |
0,997 |
19,5 |
1,001 |
1,005 |
1,004 |
0,998 |
0,992 |
0,992 |
0,996 |
20 |
1,001 |
1,005 |
1,002 |
0,996 |
0,991 |
0,992 |
0,995 |
20,5 |
1,002 |
1,004 |
1,001 |
0,995 |
0,991 |
0,994 |
0,996 |
21 |
1,003 |
1,004 |
1,001 |
0,995 |
0,993 |
0,997 |
0,996 |
21,5 |
1,004 |
1,004 |
1 |
0,996 |
0,995 |
1 |
0,995 |
22 |
1,005 |
1,004 |
0,999 |
0,996 |
0,996 |
1 |
0,997 |
22,5 |
1,006 |
1,004 |
0,999 |
0,997 |
1 |
1,004 |
1 |
23 |
1,007 |
1,003 |
0,998 |
0,998 |
1,001 |
1,006 |
1,001 |
23,5 |
1,008 |
1,003 |
0,998 |
0,999 |
1,002 |
1,007 |
1,002 |
24 |
1,007 |
1,002 |
0,997 |
1 |
1,002 |
1,008 |
1,003 |
24,5 |
1,006 |
1,001 |
0,997 |
1 |
1,002 |
1,006 |
1,003 |
25 |
1,004 |
1 |
0,996 |
1 |
1,002 |
1,004 |
1,003 |
25,5 |
1,003 |
0,998 |
0,996 |
1 |
1,002 |
1,002 |
1,002 |
26 |
1,002 |
0,997 |
0,996 |
1 |
1,002 |
1 |
1 |
Продовження таблиці
х |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0,267 |
0,275 |
0,282 |
0,29 |
0,297 |
0,304 |
0,314 |
1 |
0,519 |
0,534 |
0,547 |
0,562 |
0,575 |
0,593 |
0,603 |
1,5 |
0,74 |
0,758 |
0,776 |
0,794 |
0,813 |
0,832 |
0,844 |
2 |
0,919 |
0,938 |
0,956 |
0,974 |
0,986 |
1,003 |
1,02 |
2,5 |
0,05 |
1,067 |
1,084 |
1,09 |
1,105 |
1,12 |
1,133 |
3 |
1,13 |
1,142 |
1,154 |
1,164 |
1,172 |
1,176 |
1,178 |
3,5 |
1,161 |
1,166 |
1,171 |
1,174 |
1,175 |
1,175 |
1,175 |
4 |
1,16 |
1,161 |
1,156 |
1,149 |
1,141 |
1,131 |
1,118 |
4,5 |
1,132 |
1,127 |
1,111 |
1,099 |
1,085 |
1,071 |
1,053 |
5 |
1,084 |
1,069 |
1,053 |
1,037 |
1,019 |
1,001 |
0,986 |
5,5 |
1,032 |
1,016 |
0,994 |
0,979 |
0,962 |
0,951 |
0,932 |
6 |
0,984 |
0,956 |
0,949 |
0,934 |
0,922 |
0,92 |
0,906 |
6,5 |
0,948 |
0,936 |
0,92 |
0,91 |
0,903 |
0,903 |
0,905 |
7 |
0,927 |
0,917 |
0,911 |
0,908 |
0,909 |
0,915 |
0,925 |
7,5 |
0,922 |
0,911 |
0,92 |
0,927 |
0,934 |
0,946 |
0,958 |
8 |
0,932 |
0,936 |
0,944 |
0,955 |
0,97 |
0,986 |
1,004 |
8,5 |
0,951 |
0,958 |
0,974 |
0,99 |
1,006 |
1,023 |
1,041 |
9 |
0,976 |
0,99 |
1,006 |
1,023 |
1,039 |
1,053 |
1,061 |
9,5 |
1 |
1,015 |
1,033 |
1,048 |
1,059 |
1,066 |
1,066 |
10 |
1,02 |
1,036 |
1,049 |
1,059 |
1,063 |
1,062 |
1,056 |
10,5 |
1,033 |
1,046 |
1,054 |
1,058 |
1,055 |
1,048 |
1,033 |
11 |
1,039 |
1,047 |
1,048 |
1,044 |
1,034 |
1,021 |
1,005 |
11,5 |
1,037 |
1,043 |
1,034 |
1,024 |
1,01 |
0,994 |
0,997 |
12 |
1,027 |
1,025 |
1,015 |
1 |
0,984 |
0,96 |
0,958 |
12,5 |
1,017 |
1,01 |
0,995 |
0,979 |
0,965 |
0,954 |
0,949 |
13 |
1,005 |
0,993 |
0,98 |
0,964 |
0,955 |
0,95 |
0,955 |
13,5 |
0,995 |
0,982 |
0,968 |
0,958 |
0,954 |
0,958 |
0,97 |
14 |
0,987 |
0,974 |
0,965 |
0,961 |
0,965 |
0,976 |
0,99 |
14,5 |
0,983 |
0,97 |
0,969 |
0,971 |
0,981 |
0,997 |
1,01 |
15 |
0,983 |
0,976 |
0,978 |
0,987 |
1,001 |
1,017 |
1,03 |
15,5 |
0,985 |
0,984 |
0,991 |
1,003 |
1,019 |
1,032 |
1,04 |
16 |
0,99 |
0,993 |
1,003 |
1,018 |
1,031 |
1,039 |
1,039 |
16,5 |
0,995 |
1,001 |
1,014 |
1,027 |
1,036 |
1,038 |
1,028 |
17 |
0,999 |
1,008 |
1,02 |
1,03 |
1,032 |
1,027 |
1,012 |
17,5 |
1,002 |
1,012 |
1,023 |
1,027 |
1,023 |
1,013 |
0,988 |
18 |
1,004 |
1,014 |
1,02 |
1,018 |
1,008 |
0,993 |
0,979 |
18,5 |
1,003 |
1,012 |
1,014 |
1,007 |
0,993 |
0,978 |
0,969 |
19 |
1,004 |
1,009 |
1,006 |
1,007 |
0,981 |
0,969 |
0,956 |
19,5 |
1,003 |
1,005 |
0,998 |
0,985 |
0,973 |
0,967 |
0,973 |
20 |
1,003 |
1,001 |
0,991 |
0,979 |
0,972 |
0,974 |
0,985 |
20,5 |
1,001 |
0,996 |
0,986 |
0,976 |
0,974 |
0,99 |
1,001 |
21 |
0,999 |
0,993 |
0,983 |
0,975 |
0,981 |
1,002 |
1,016 |
21,5 |
0,998 |
0,992 |
0,986 |
0,988 |
0,997 |
1,013 |
1,024 |
22 |
0,997 |
0,991 |
0,991 |
0,997 |
1,012 |
1,024 |
1,029 |
22,5 |
0,996 |
0,992 |
0,998 |
1,008 |
1,022 |
1,028 |
1,026 |
23 |
0,997 |
0,994 |
1,002 |
1,015 |
1,025 |
1,027 |
1,016 |
23,5 |
0,998 |
0,997 |
1,007 |
1,017 |
1,023 |
1,023 |
1,002 |
24 |
0,999 |
1 |
1,008 |
1,017 |
1,015 |
1,012 |
0,988 |
24,5 |
1 |
1,002 |
1,008 |
1,014 |
1,005 |
0,995 |
0,979 |
25 |
1,001 |
1,003 |
1,005 |
1,008 |
0,991 |
0,985 |
0,975 |
25,5 |
1,002 |
1,004 |
1,004 |
1,001 |
0,986 |
0,978 |
0,977 |
26 |
1,002 |
1,004 |
1,002 |
0,987 |
0,984 |
0,977 |
0,983 |