4 Розрахунок оптимальних настройок беперервного регулятору

Приблизні настройки регулятора за перехідною характеристикою визначаються за методом А.П. Копеловича. Згідно з цим методом настройки регуляторів розраховують за формулами наведеними в табл. 4.1, з урахуванням обраного типу перехідного процесу.

Таблиця 4.1 Настройки регуляторів на статичних об’єктах

Регулятор	Тип перехідного процесу
І
П
ПІ
ПІД

З метою отримання більш точних настройок їх розрахунок виконується на базі АФХ об’єкта керування. При цьому досягається завданий характер затухання перехідного процесу в замкнутій системі, який характеризується показником коливання (М). Значення показника (М), як правило, обирають у межах 1,1-2,4. При цьому для = 20% М 1,3, для = 40% М 2,1. Обираючи значення (М), можливо задати бажаний характер перехідного процесу в системі.

Метод графічного розрахунку настройок заснований на тому, що АФХ розімкнутої системи регулювання, що може бути розрахована як , повинна торкатися кола, яке є геометричним місцем точок із завданим значенням (М). Радіус такого кола , а її центр розташований на від’ємній дійсній півосі на відстані (рис. 4.1).

Рис. 4.1 Визначення заданого характеру затухання перехідного процесу

В залежності від закону регулювання змінюються настройки регуляторів.

П-регулятор. Будують АФХ розімкнутої системи з П-регулятором, коефіцієнт підсилення якого дорівнює одиниці:

(4.1)

АФХ розімкнутої системи співпадає з АФХ об’єкта.

АФХ об’єкта будують у відповідності з наведеною нижче методикою. Передаточна функція об’єкта в загальному випадку має вигляд:

(4.2)

З метою отримання частотної передаточної функції змінюють р на :

(4.3)

Наступний крок – відокремлення уявної та дійсної частин окремо в чисельнику і знаменнику частотної передаточної функції. В такому разі враховують, що j² = -1, j⁴ = 1, j⁶ = -1, j⁸ = 1. В дійсній частині уявна одиниця зникає, а в уявній її треба винести за дужки. Частотна передаточна функція набуває вигляд суми дійсної (U) та умовної (jV) складових у чисельнику та знаменнику:

, (4.4)

де - дійсна складова поліному чисельника, - уявна складова поліному чисельника, - дійсна складова поліному знаменника, - уявна складова поліному знаменника.

З урахуванням прийнятих позначень АФХ об’єкту можна розрахувати:

, , (4.5)

де – модуль чисельника передаточної функції об’єкта, – модуль знаменника передаточної функції об’єкта, – аргумент чисельника передаточної функції об’єкта, – аргумент знаменника передаточної функції.

, ,

, (4.6)

За отриманими данними на комплексній площині для кожного значення частоти () будують декілька векторів з модулем і аргументом . Кінці векторів з’єднують плавною кривою, яка і є амплітудно-фазовою характеристикою об’єкта (див. рис. 4.2).

Рис. 4.2 Побудова АФХ об’єкта у полярній системі координат

Якщо передаточну функцію (4.2) можна представити як сума дійсної та уявної складових:

, (4.7)

то завдаючи набір значень частоти ( ) для кожного з розрахованих значень дійсної та уявної складової передаточної функції отримають набір точок, з’єднавши їх, отримують АФХ( рис. 4.3).

Рис. 4.3 Побудова АФХ об’єкта у декартовій системі координат

У якості першого наближення при виборі частоти ( ) рекомендується вибрати значення, що розраховується у відповідності з виразом:

(4.8)

Рекомендується для обраного значення частоти розрахувати модуль та аргумент АФХ та побудувати його на комплексній площині. Отримана точка аналізується та приймається рішення про вибір наступного значення частоти. Кількість точок, для яких розраховується АФХ а також їх шах студент визначає самостійно з урахуванням того, щоб АФХ охоплювала (I-IV) квадранти та була плавно відображена на комплексній площині.

Далі з початку координат під кутом до від’ємної півосі проводять промінь. За допомогою циркуля проводять коло з центром на від’ємній дійсній півосі, яке разом торкається цього променя та АФХ. Вимірюють радіус кола (R) у тих самих одиницях, в яких будується АФХ (рис. 4.1). Коефіцієнт підсилення П- регулятора визначають за формулою:

(4.9)

І-регулятор. Будують АФХ об’єкта. АФХ розімкнутої системи з І-регулятором при визначається за формулою:

(4.10)

Для отримання АФХ розімкнутої системи кожен вектор АФХ об’єкта повертається за годинниковою стрілкою і зменшується в ( ) разів. Коефіцієнт підсилення визначають аналогічно П-регулятора.

В наслідок того, що використання систем з подібним регулятором обмежене і у даній роботі вони не використовуються, то наводиться лише спрощене пояснення, щодо побудови таких систем.

ПІ-регулятор. Через те що ПІ-регулятор має два настроєчних параметри, будують декілька АФХ розімкнутої системи при К_р = 1 і різних значеннях Т_і. Набір значень Т_і обирають таким чином, щоб вони складали приблизно 60, 80, 100, 120 та 140 відсотків від Т_і, отриманого за методом А.П. Копеловича. АФХ розімкнутої системи з ПІ-регулятором при К_р = 1 для обраного значення Т_і визначається за формулою:

(4.11)

Для отримання АФХ розімкнутої системи до кожного вектора АФХ об’єкта додається вектор з модулем , повернутий на 90 за годинниковою стрілкою (рис. 4.4).

Рис. 4.4 Побудова АФХ розімкнутої системи з ПІ- регулятором

При виконанні розрахунку АФХ необхідно представити всі математичні перетворення, що було виконано відносно первинної передаточної функції. Записати вихідні вирази для виконання подальших розрахунків, а результати розрахунків представити у табличній формі (наприклад, табл. 4.1). Порядок оформлення та представлення текстового та графічного матеріалу стосується і усіх наступних розрахунків.

Таблиця 4.1 Результати розрахунку АФХ розімкнутої системи

	об()	Аоб()	А()
			Ті1	…	Тіn
1
…
n

Побудуємо нову межу ділянки стійкості у площині параметрів (К_р – Т_і). Параметр К_р визначають за відповідною АФХ аналогічно П-регулятору. Оптимальне сполучення настройок отримують в точці торкання до цієї кривої дотичної, проведеної з початку координат (рис. 4.5) з координатами (0,0).

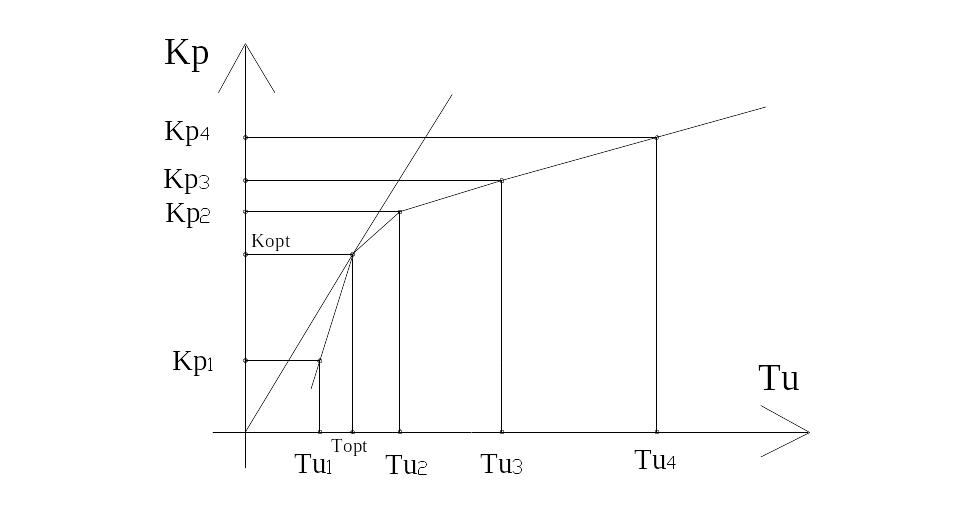
Рис. 4.5 Визначення оптимальних настройок розімкнутої системи

з ПІ-регулятором

ПІД-регулятор. При наявності трьох настроєчних параметрів час попередження Т_п приймають як частку від часу інтегрування (звичайно обирають Т_п = 0,5Т_i). Тобто сприймається як постійна. Таким чином для визначення настройок ПІД-регулятора можливо використати ту ж саму методику, що й для ПІ-регулятора. АФХ розімкнутої системи з ПІД-регулятором будується:

(4.12)

Для отримання АФХ розімкнутої системи з ПІД-регулятором будують АФХ об’єкта, після чого для обраного Т_і (отже й Т_п) до кожного вектора АФХ об’єкта додається вектор з модулем:

, (4.13)

повернутий на 90 за годинниковою стрілкою. Далі, визначають оптимальні настройки аналогічно ПІ-регулятору у площині параметрів (К_р – Т_і).