МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД

«УКРАЇНСЬКИЙ ДЕРЖАВНИЙ ХІМІКО-ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ»

2559

МЕТОДИЧНІ ВКАЗІВКИ

ДО ВИКОНАННЯ КУРСОВОЇ РОБОТИ

З КУРСУ “ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ”

для студентів з напрямку підготовки 6.050202

«Автоматизація та комп'ютерно-інтегровані технології»

Затверджено на засіданні

кафедри автоматизації

виробничих процесів.

Протокол № 9 від 19.06.2012.

Дніпропетровськ УДХТУ 2013

Методичні вказівки до виконання курсової роботи з курсу “Теорія автоматичного керування” для студенті з напрямку підготовки 6.050202 «Автоматизація та комп’ютерно-інтегровані технології» / Укл.: О.І. Швачка, О.В. Лещенко. – Дніпропетровськ: ДВНЗ УДХТУ, 2012. – 26 с.

Укладачі: О.І. Швачка

О.В. Лещенко, канд. техн. наук

Відповідальний за випуск О.П. Мисов, канд. техн. наук

Навчальне видання

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ КУРСОВОЇ РОБОТИ

З КУРСУ “ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ”

для студентів з напрямку підготовки 6.050202

«Автоматизація та комп'ютерно-інтегровані технології»

Укладачі: ШВАЧКА Олександр Іванович

ЛЕЩЕНКО Олена Василівна

Авторська редакція

Підписано до друку 25.02.13. Формат 60×84 1/16. Папір ксерокс. Друк різограф.

Умовн.-друк. арк. 1,11. Облік.-вид. арк. 1,14. Тираж 70 прим. Замов. № 209. Свідоцтво ДК № 303 від 27.12.2000 р.____________________________________

ДВНЗ УДХТУ, 49005, м. Дніпропетровськ, 5, просп. Гагаріна, 8______________

Видавничо-поліграфічний комплекс ІнКомЦентру

ЗМІСТ

	Вступ	4
1	Зміст та обсяг курсової роботи	5
2	Отримання передаточної функції об’єкт керування	6
3	Вибір закону регулювання	9
4	Розрахунок оптимальних настройок безперервного регулятора	12
5	Оцінка сталості системи з оптимальними настройками	18
6	Оцінка якості замкнутої системи	19
	Список літератури	23
	Додатки	25

ВСТУП

Теорія автоматичного керування є основною науковою базою для дослідження та проектування любих автоматичних та автоматизованих систем в усіх галузях техніки. Системи автоматичного керування відрізняються об’єктами керування та призначенням, а також по фізичній природі сигналів у регуляторах. Але всі ці суттєві відзнаки мають лише другорядне значення при дослідження динамічних властивостей систем керування. Важлива не фізична природа сигналів у системах керування, а інформація, що у ній передається. В результаті можливим є розділення системи автоматичного керування на окремі функціональні елементи та проведення аналізу та синтезу системи з використанням типових ланок.

Метою курсової роботи є засвоєння методів аналіз та синтезу безперервних систем керування, що охоплені зворотнім зв’язком. Тобто, окремі пристрої системи можуть бути розраховані та бути працездатні, але утворювати непрацездатну систему. Тому у процесі проектування необхідно дослідити динамічні властивості замкнутих систем керування. Для реалізації поставлених задач у курсовій роботі поставлені такі питання як визначення передаточної функції системи за її структурною схемою, визначення стійкого стану системи, розрахунок і побудова частотних характеристик, визначення показників якості перехідного процесу.

1 Зміст та обсяг курсової роботи

Курсова робота на тему «Синтез безперервної АСР» складається з наступних розділів:

1. Визначення динамічних характеристик об’єкта керування та отримання передаточної функції об’єкта за кривою розгону по каналу регулювання

2. Вибір закону регулювання у відповідності до встановлених вимог, що пред’являються до роботи автоматичної системи

3. Розрахунок оптимальних настройок регулятора у відповідності з обраним характером перехідного процесу

4. Оцінка сталості системи з оптимальними настройками з використанням частотних критеріїв стійкості

5. Оцінка показників якості системи з оптимальними настройками по кривій перехідного процесу

Загальні вимоги по складу пояснювальної записки:

• титульний аркуш;

• лист завдання загальноприйнятого зразка;

• лист індивідуального завдання (крива розгону по каналу регулювання);

• текст пояснювальної записки;

• висновки по результатам виконання курсової роботи;

• список використаної літератури;

• додатки (таблиці, рисунки).

Пояснювальна записка повинна бути викладена українською мовою у обсязі 30-40 сторінок. Вимоги по набору тексту: шрифт - Times New Roman, розмір - 14, відступи зліва - 3 см, з права, знизу та зверху 2 см; інтервал - 1,5; формули набрано за допомогою редактора Microsoft Equation 3.0; назви розділів оформлювати напівжирним шрифтом розміром 16; підрозділи напівжирним курсивом розміром 14.

При необхідності роботи з діаграмами та схемами за методичними вказівками нема потреби переносити їх в текст пояснювальної записки, але необхідно вказати отримані результати та відповідне посилання на літературне джерело. За результатами виконання окремих етапів роботи мають бути побудовані графічні характеристики. При цьому, необхідно зазначити найменування осей а також прийняту розмірність по кожній з них. Зміст графічного матеріалу повинен пояснювати підрисуночний підпис. Також заголовки повинні мати таблиці з результатами розрахунків. Всі скорочення та позначення, що відрізняються від загальноприйнятих, повинні бути пояснені в тексті записки.

2 Отримання передаточної функції обєкта керування

Передаточна функція об’єкта керування може бути отримана шляхом обробки кривої розгону або імпульсної характеристики. Якщо задана імпульсна характеристика, то необхідно перебудувати її у криву розгону. Імпульсну вхідну дію можна розглядати як суму двох дій однакової амплітуди та різних напрямків, які зміщені відносно одне одного на інтервал часу . У такому випадку імпульсна перехідна функція описується рівнянням:

(2.1)

тобто

(2.2)

У відповідності до (2.2) точки кривої розгону та імпульсної характеристики на інтервалі часу [0; ] співпадають . Од же, наступні точки кривої розгону будуються таким чином:

	…

Для визначення алгоритму функціонування (закону регулювання) та отримання приблизних настройок регулятору (за методом А.М. Капеловича) [1] передаточну функцію об’єкта представимо у вигляді добутку передаточної функції аперіодичної ланки першого порядку та ланки запізнювання, наприклад для статичного об’єкту передаточна функція має вигляд:

, (2.3)

де k_о – коефіцієнт передачі об’єкта, одиниця вимірювання вихідної змінної (% ходу регулюючого органа); Т_о – постійна часу, одиниця часу; _о– повне запізнювання, одиниця часу.

Для астатичного об’єкту передаточна функція має вигляд:

(2.4)

Коефіцієнт передачі об’єкта визначається як відношення зміни вихідної величини (∆у) до зміни вхідної величини (∆х).

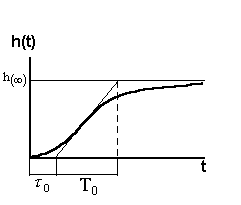
Постійна часу та повне запізнювання визначається з використанням одного з методів, викладених у [2-4]: метод дотичної, метод Ормана, логарифмічного усереднення та інші. Наприклад, за допомогою методу дотичної постійна часу та повне запізнювання для статичного об’єкта визначаються як показано на рис. 2.1. Слід звернути увагу, що до кривої необхідно побудувати дотичну до точки, де відбувається зростання параметру з максимальною швидкістю. Інтервал часу, що відповідає перетини дотичної з початковим та кінцевим станом системи відповідає постійній часу.

а) для статичних об’єктів	б) для астатичних об’єктів
Рис. 2.1 Визначення постійної часу та часу повного запізнювання

Постійна часу для астатичних об’єктів визначається:

(2.5)

Точніше визначення передаточної функції статичних об’єкта виконується за допомогою методу площин (метод М.П. Симою [1]), метод додаткових членів [5], або іншого методу.

Згідно з методом додаткових членів початкова крива розгону нормується шляхом ділення на величину h( ) кожної ординати. Вісь ординат зміщують вправо на величину чистого запізнення (чисте запізнювання відповідає часу від моменту нанесення збурення, протягом якого не відбувається зміни вихідної величини), після чого знаходять h(t₁)=0,6321 (рис. 2.2). Інтервал часу t₂ визначається як t₁/2.

Рис. 2.2 Визначення параметрів передаточної функції за методом

додаткових членів

На кривій розгону визначають точку h(t₂), після чого за графіком, наведеним на рис. 2.3 визначають порядок передаточної функції.

h(t₂)

n

Рис. 2.3 Визначення порядку уточненої передаточної функції

В залежності від порядку передаточної функції (n) визначають значення коефіцієнта D_n. (табл. 2.1)

Таблиця 2.1 Показники коефіцієнту D_n для визначення постійних часу

n	1	2	3	4	5	6	7
Dn	0,962	0,642	0,524	0,462	0,421	0,391	0,371

З урахуванням коефіцієнта D_n постійні часу визначають за формулами:

; , … (2.6)

Отримана таким чином передаточна функція об’єкта має вигляд:

(2.7)

Згідно з методом М.П. Симою (метод площин) безрозмірна передаточна функція статичного об’єкту (без чистого запізнювання) визначається:

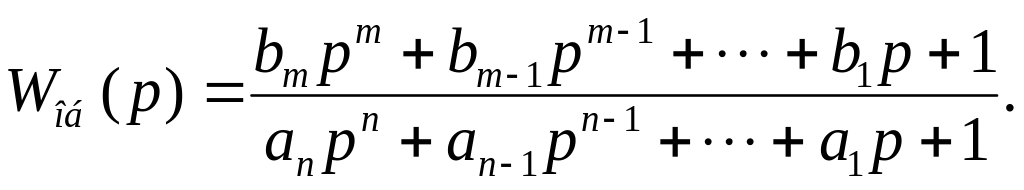(2.8)

Коефіцієнти рівняння (2.8) визначаються з системи:

(2.9)

де , при , та при , .

Площини F₁, F₂, . . . F_i обчислюють з наступної системи:

(2.10)

де - середнє значення вихідної величини об’єкту.

На практиці обмежуються обчисленням площин не вище четвертого порядку.

Після обчислення площин складають систему рівнянь (2.9) з урахуванням вигляду і порядку (n) характеристичного поліному передаточної функції. Якщо , то . При , :

; ; (2.11)

В разі від’ємного знаку якої-небудь площини , порядок характеристичного поліному передаточної функції , а порядок полінома чисельника передаточної функції (m) підвищується на одиницю. У випадку коефіцієнти передаточної функції розраховують за формулами:

; ; ; (2.12)

Розрахунок площин , …, необхідно виконувати з використанням [7]. Для отримання розмірної передаточної функції безрозмірну передаточну функцію необхідно помножити на коефіцієнт передачі , визначений як було наведено вище. Чисте запізнення враховується множенням розмірної передаточної функції на .