Контрольная работа № 2
Рассчитать переходный процесс схемы по методу переменных состояния.
Принципиальная схема
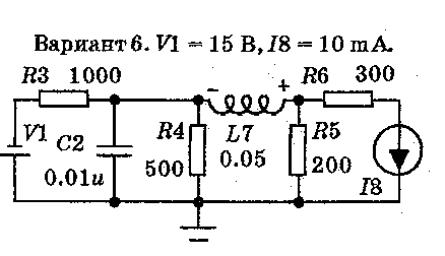
Исходные данные:
V1 = 15 В
I8 = 10 мА
R3 = 1000 Ом
R4 = 500 Ом
R5 = 200 Ом
R6 = 300 Ом
C2 = 0,01 u мкФ
L7 = 0,05 Гн
Графом электронной схемы называется скелетная схема, изображающая топологию элементов схемы, т.е. соединения элементов между собой. Вершины графа соответствуют узлам схемы, ребра – отдельным элементам.
Построим эквивалентную схему.
Рис. 1. Эквивалентная схема
Рис. 2. Граф эквивалентной схемы
Рис. 3. Собственное дерево графа и главные сечения
Строим дерево графа с ветвями и хордами для того, чтобы построить матрицу главных сечений.
Рис. 4. Дерево графа с ветвями и хордами
Теперь строим матрицу главных сечений графа.
Матрица главных сечений может быть представлена как:
где Е – единичная матрица, которая является матрицей главных сечений для ветвей.
Матрица главных сечений используется для записи алгебраических уравнений по первому закону Кирхгофа:
Систему уравнений можно представить как:
или 
Вектор токов I состоит из
двух подвекторов: вектора токов ветвей
и вектора токов хорд
.
Уравнение выражает зависимость токов ветвей через токи хорд. Для рассматриваемой схемы:
Теперь строим матрицу главных контуров.
Отсюда составляем систему уравнений:
Систему можно представить в виде произведения Ак на вектор-столбец напряжений U:
или
Вектор напряжения U состит из двух подвекторов – вектора напряжений ветвей Uв и вектора напряжений хорд Uх:
Уравнение преобразуется к виду:
или
Для рассматриваемой схемы запишем уравнение в виде:
Топологическое уравнение цепи и реализация метода переменных состояния.
Уравнения, полученные путем использования первого и второго законов Кирхгофа (система уравнения для токов и напряжений) объединяется в одно матричное уравнение:
Для уменьшения числа уравнений в системе, полностью описывающей поведение электронной схемы с динамическими реактивными элементами С и L, переходим с помощью топологической системы уравнений и компонентных уравнений к системе уравнений переменных состояния (это токи в индуктивностях L и напряжение на емкостях). Обозначаем вектор переменных состояния через Х. Тогда, если схема имеет m индуктивностей и n емкостей, то число составляющих ветора Х, т.е. порядок системы уравнений переменных состояния, будет m+n. В общем виде для динамических элементов компонентные уравнения в общем виде можно записать как:
или
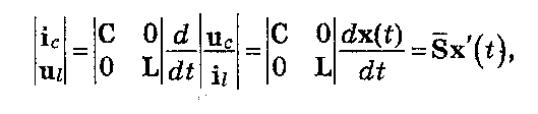
где
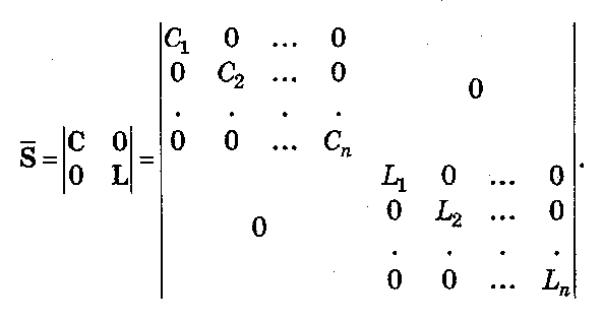
Выразим токи
через матрицу F, поскольку
емкости входят в ветви
,
откуда
.
Аналогично с
,
откуда
,
где
и
- те строки матриц
и
,
которые относятся к емкостям и
индуктивностям.
Полную систему можно записать в виде:
Для нашего задания полная топологическая система уравнений в раскрытом виде с обозначениями типов элементов запишется следующим образом.
Для токов:
И для напряжений:
Переменными состояния в нашей схеме
являются
и
.
Через них выразим токи и напряжения
резисторов
,
,
,
,
входящие в вышеприведенную систему
уравнений. Получаем:
,
,
,
Подставляя в выражение для , получим:
Подобным образом находим
Из компонентных уравнений для реактивных элементов С2 и L7:
,
,
получаем систему из двух обыкновенных дифференциальных уравнений в форме Коши:
Применим явный метод численного интегрирования Эйлера для решения ОДУ. В соответствии с этим методом:
,
.
где
- интервал дискретизации по осям времени
или шаг численного интегрирования;
,
- значения переменных состояния на n-м
шаге интегрирования;
,
- значения переменных состояния на
(n-1)-м шаге численного
интегрирования.
В результате получим систему из двух рекуррентных алгебраических выражений:
где в качестве начальных условий можно
принять нулевые начальные условия
.
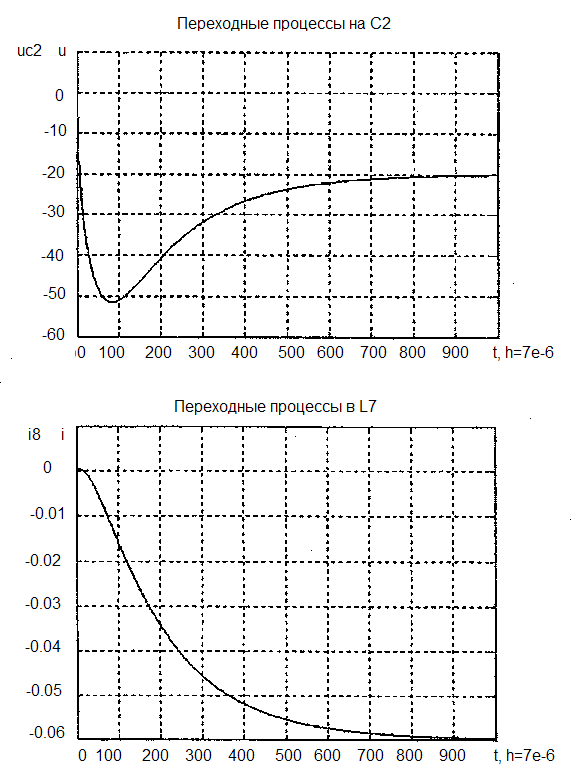
Программа расчета переходного процесса (MatLab).
Шаг интегрирования
.
%Лабораторная работа моделирование
%Присвоение номинальных значений компонентам схемы
e1=15; i8=10e-3; r3=1000; r4=500;
r5=200; r6=300; c2=0.01e-6; l7=0.05;
h=7e-6
%Присвоение нулевых начальных условий переменным состояния
uc2=zeros(1,1000); i7=zeros(1,1000);
%Расчет переходного процесса путем организации цикла для расчета переменных состояния
for i=2:1000
uc2(1,i)=uc2(1,i-1)+h/r3*((-e1-uc2(1,i-1))/r5+(-e1-uc2(1,i-1)
-uc2(1,i-1))/r6-uc2(1,i-1)/r3-l7(1,i-1)-i8);
uc2(1,i)=uc2(1,i-1)+h/c2*((-e1-uc2(1,i-1))/r6:
l7(1,i)=i7(1,i-1)+h/i8*(-e1+uc2(1,i-1)-i8);
end
%Построение графиков
i=1:1:1000;
plot(l, uc2, ’r’, ‘g’)
grid
title (‘Переходные процессы на C2);
xlabel (‘t, h=7e-6’);
ylabel (‘uc2’);
figure
plot (l, i7, ‘b’);
grid
title (‘Переходные процессы в L7’);
xlabel (‘t, h=7e-6’);
ylabel (‘i8’)
