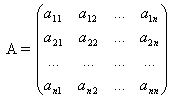Контрольное задание № 1

1. Что такое след квадратной матрицы?

След матрицы — операция, отображающая пространство квадратных матриц в поле, над которым определена матрица (для действительных матриц — в поле действительных чисел, для комплексных матриц — в поле комплексных чисел). След матрицы — это сумма элементов главной диагонали матрицы, то есть если элементы матрицы , то её след .

2. Вычислить след матрицы по заданию.

(вариант 6)

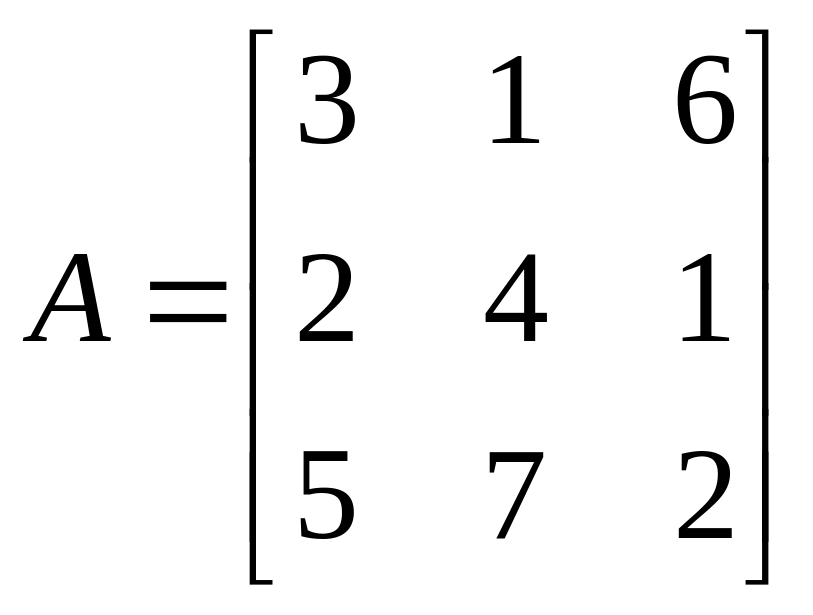
tr (А) = 3 + 4 + 2 = 9

3. Что такое определитель матрицы?

Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:

, где М1k - определитель матрицы (детерминант), полученной из исходной матрицывычеркиванием первой строки и k - oго столбца. Следует обратить внимание на то, чтоопределители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. Первая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя матрицы по первому столбцу:

Вообще говоря, определитель матрицы может вычисляться по любой строке или столбцуматрицы, т.е. справедлива формула:

Очевидно, что различные матрицы могут иметь одинаковые определители. Определитель единичной матрицы равен 1. Для указанной матрицы А число М1k называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Дополнительный минор произвольного элемента квадратной матрицы aij равенопределителю матрицы, полученной из исходной матрицы вычеркиванием i-ой строки и j-го столбца.

4. Вычислить определитель матрицы произведения двух матриц.

Для начала произведем операцию умножения матриц А и В.

Теория:

Даны две прямоугольные матрицы и размерности и соответственно:

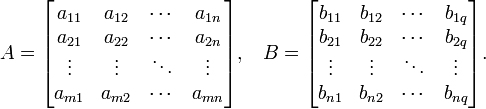
Тогда матрица размерностью называется их произведением:

где:

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Решение:

Есть 2 матрицы: А (3 × 3) и В (3 × 3). Следовательно в результате умножения этих двух матриц получится матрица: С (3 × 3). Рассчитаем по правилу умножения матриц коэффициенты новой матрицы: С (3 × 3).

С 11 = (3) × (1) + (1) × (7) + (6) × (3) = 28 С 12 = (3) × (2) + (1) × (5) + (6) × (6) = 47 С 13 = (3) × (1) + (1) × (3) + (6) × (2) = 18 С 21 = (2) × (1) + (4) × (7) + (1) × (3) = 33 С 22 = (2) × (2) + (4) × (5) + (1) × (6) = 30 С 23 = (2) × (1) + (4) × (3) + (1) × (2) = 16 С 31 = (5) × (1) + (7) × (7) + (2) × (3) = 60 С 32 = (5) × (2) + (7) × (5) + (2) × (6) = 57 С 33 = (5) × (1) + (7) × (3) + (2) × (2) = 30 Т. к. С 11 = (А 11) × (В 11) + (А 12) × (В 21) + (А 13) × (В 31) = С 11 С 12 = (А 11) × (В 12) + (А 12) × (В 22) + (А 13) × (В 32) = С 12 С 13 = (А 11) × (В 13) + (А 12) × (В 23) + (А 13) × (В 33) = С 13 С 21 = (А 21) × (В 11) + (А 22) × (В 21) + (А 23) × (В 31) = С 21 С 22 = (А 21) × (В 12) + (А 22) × (В 22) + (А 23) × (В 32) = С 22 С 23 = (А 21) × (В 13) + (А 22) × (В 23) + (А 23) × (В 33) = С 23 С 31 = (А 31) × (В 11) + (А 32) × (В 21) + (А 33) × (В 31) = С 31 С 32 = (А 31) × (В 12) + (А 32) × (В 22) + (А 33) × (В 32) = С 32 С 33 = (А 31) × (В 13) + (А 32) × (В 23) + (А 33) × (В 33) = С 33

Ответ:

* =

Теперь вычислим определитель этой матрицы:

det C = -288