2.3 Наклеп

Если в процессе растяжения дойти до некоторой точки М на диаграмме, а затем начать разгрузку, то зависимость между напряжением и продольной деформацией будет выражаться прямой MN, параллельной упругому участку OB. При полном снятии нагрузки в образце сохраняется остаточная деформация _ост = ON. Полная деформация испытываемого образца состоит из упругой деформации _упр = NN, исчезающей при разгрузке, и остаточной _ост = ON:

.

Если затем снова начать нагружение, то до напряжения, при котором начата разгрузка зависимость между напряжением и деформацией будет изображаться прямой NM, а при дальнейшем увеличении нагрузки эта зависимость пойдет по прежней кривой MEK, по которой она шла бы без разгрузки. Таким образом, при повторном нагружении, материал ведет себя как линейно упругий до напряжения _М.

Это повышение предела пропорциональности, вызванное предварительным нагружением материала за предел текучести, называется деформационным упрочнением, наклепом или нагартовкой.

2.4 Диаграммы растяжения других конструкционных материалов

Р

Рисунок 2.4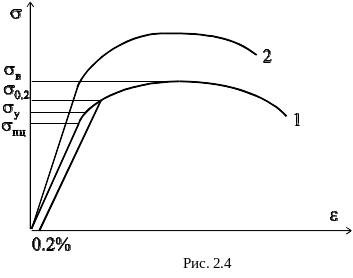

ассмотрим диаграммы растяжения некоторых других конструкционных материалов (рис. 2.4), имеющих широкое распространение в машиностроении: 1  диаграмма растяжения алюминиевого сплава Д-16; 2  диаграмма растяжения низколегированной стали.

Как и Ст3, эти материалы при растяжении получают значительные остаточные деформации и разрушаются с образованием шейки. Однако их диаграммы растяжения не имеют ярко выраженной площадки текучести. Поэтому в этом случае вводят понятие условного предела текучести, за который принимают напряжение, при котором остаточная деформация составляет 0,2 %. Условный предел текучести обозначают через _0,2.

Р

Рисунок 2.5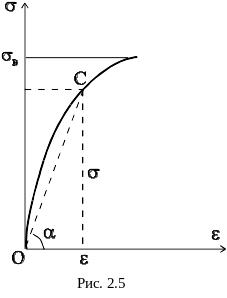

ассмотрим диаграмму растяжения серого чугуна СЧ 28 (рис. 2.5). Чугун является хрупким материалом, и разрыв образца происходит при незначительном удлинении и без образования шейки. Диаграмма не имеет начального прямолинейного участка. Однако, определяя деформации в чугунных деталях, пользуются законом Гука:  = Е. Значение модуля упругости Е находят как тангенс угла наклона прямой, проведенной через начальную точку О диаграммы и точку С, соответствующую напряжению, при котором определяют деформацию.

Такой модуль упругости называют секущим:

.

2.5 Испытание конструкционных материалов на сжатие

Испытание материалов на сжатие проводят на специальных прессах или универсальных испытательных машинах. Образцы для испытаний на сжатие металлов имеют вид коротких цилиндров с отношением высоты к диаметру 2/3. Образцы из бетона, дерева, цемента и т.п. изготавливают в виде куба или параллелепипеда небольшой высоты.

П

Рисунок 2.6

ри испытании на сжатие для пластичных материалов можно определить пределы пропорциональности, упругости и текучести, а для хрупких  предел прочности. Предел прочности для пластичных материалов не определяют, т.к. образец из пластичного материала при сжатии не разрушается, а сплющивается в диск при непрерывном возрастании сжимающей силы. Диаграмма сжатия пластичного материала (сталь) показана на рис. 2.6.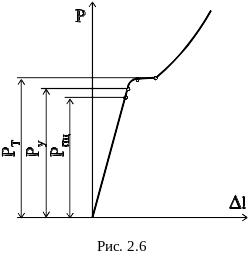

Испытание прекращают при некоторой нагрузке, вызывающей заметную пластическую осадку образца. Образец принимает бочкообразную форму, что связано с влиянием сил трения на торцах образца. Эти силы трения препятствуют поперечным перемещениям частиц материала вблизи торцов образца.

О

Рисунок 2.7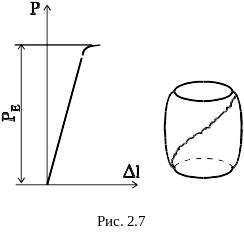

бразцы из хрупкого материала при испытании на сжатие доводят до разрушения, определяя разрушающую нагрузку Р_в и предел прочности материала при сжатии: _в = Р_в/F₀.

Образцы из хрупкого материала при сжатии разрушаются при малых остаточных деформациях с образованием наклонных или продольных трещин. Диаграмма сжатия чугуна СЧ 28 представлена на рис. 2.7.

Большинство конструкционных материалов работает на сжатие существенно лучше, чем на растяжение, то есть для таких материалов . Чугунный образец разрушается с образованием трещины под углом 45 к продольной оси образца, то есть по площадке, где действуют максимальные касательные напряжения _max.