Лекция 2 Опытное изучение механических свойств материалов

Опытное изучение свойств материалов при одноосном растяжении; диаграмма растяжения стали марки Ст3; наклеп; диаграммы растяжения других конструкционных материалов; испытание конструкционных материалов на сжатие; определение твердости; деформации при растяжении (сжатии)

При проектировании и расчетах деталей машин и элементов сооружений на прочность, жесткость и устойчивость необходимо знать свойства материалов.

Основные свойства конструкционных материалов выявляются в процессе опытов с образцами, выполненными из этих материалов. Материалы испытывают на растяжение, сжатие, сдвиг, кручение, изгиб (классификация по видам деформации) и определяют их твердость. Количественные характеристики свойств материалов, устанавливаемые в результате этих механических испытаний называют механическими характеристиками.

По характеру приложения внешних сил испытания разделяются на статические, динамические (ударной нагрузкой) и испытания на выносливость (нагрузкой, вызывающей напряжения, переменные во времени).

2.1 Опытное изучение свойств материалов при одноосном растяжении

О

Рисунок 2.1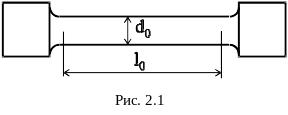

дним из основных видов испытаний материалов является статическое испытание на одноосное растяжение. Из испытуемого материала изготавливают специальные образцы. Чаще всего их делают цилиндрическими (рис. 2.1), из листового материала обычно изготавливают призматические образцы.

В цилиндрических образцах должно быть выдержано соотношение между расчетной длиной образца l₀ и диаметром d₀: у длинных образцов l₀ = 10 d₀; у коротких l₀ = 5 d₀. В качестве основных применяют образцы с диаметром d₀ = 10 мм; при этом расчетная длина l₀ = 100 мм.

Стандартные призматические образцы прямоугольного поперечного сечения имеют ширину, втрое большую толщины, а расчетную длину , где F₀  площадь поперечного сечения.

Испытания образцов проводятся на разрывных или универсальных испытательных машинах с механическим или гидравлическим силообразованием. Испытательная машина снабжена диаграммным аппаратом, который в процессе испытания вычерчивает график зависимости между осевой силой P, растягивающей образец, и соответствующим удлинением образца l  диаграмму растяжения Р = f(l).

2.2 Диаграмма растяжения стали марки Ст3

Рассмотрим характерные участки и точки диаграммы растяжения малоуглеродистой стали, а также соответствующие им стадии деформирования образца (рис. 2.2).

От начала нагружения до определенного значения растягивающей силы имеет место прямая пропорциональная зависимость между силой и удлинением образца. Эта зависимость выражается на диаграмме прямой ОА. На этой стадии растяжения справедлив закон Гука. Обозначим силу, при которой закон пропорциональности прекращает свое действие, через Р_пц. Этому значению силы на диаграмме соответствует точка А. Напряжение, вызванное силой Р_пц, называется пределом пропорциональности и вычисляется по формуле: _пц = Р_пц/F₀.

Пределом пропорциональности _пц называется напряжение, после которого нарушается закон Гука. Для Ст3 _пц  200 МПа.

Деформация называется упругой, если она полностью исчезает после разгрузки. Постепенно повышая нагрузку, будем проводить полную разгрузку образца. Пока сила Р не достигнет определенной величины, вызванные ею деформации будут исчезать при разгрузке. Процесс разгружения при этом изобразится той же линией, что и нагружение. Обозначим через Р_у наибольшее значение силы, при котором образец еще не дает при разгрузке остаточной деформации. Этому значению на диаграмме соответствует точка В, а упругой стадии растяжения образца  участок ОВ.

Наибольшее напряжение, до которого остаточная деформация образца не обнаруживается при разгрузке, называется пределом упругости _у = Р_у /F₀. Обычно за предел упругости принимают напряжение, при котором остаточная деформация достигает 0,0010,005 %. При этом предел упругости обозначается через _0,001 или _0,005. Для Ст3 _у  210 МПа.

Далее кривая плавно поднимается до точки C, где наблюдается переход к горизонтальному участку CD, называемому площадкой текучести. На этой стадии удлинение образца растет при постоянном значении растягивающей силы, обозначаемой Р_т. Такой процесс деформации называется текучестью материала.

Пределом текучести называется наименьшее напряжение, при котором деформация образца происходит при постоянном растягивающем усилии, _т = Р_т /F₀. Для Ст3 _т = 240 МПа.

После стадии текучести материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации. Этому процессу соответствует восходящий участок DE диаграммы, называемый участком упрочнения. Точка E соответствует наибольшему усилию Р_max, которое может воспринять образец.

Напряжение, соответствующее максимальной силе Р_max, называется временным сопротивлением или пределом прочности _в = Р_max /F₀. Для Ст3 _В  400 МПа.

После достижения усилия Р_max деформация происходит на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки и к падению силы Р, не смотря на то, что напряжение в сечении шейки непрерывно растет.

Обозначив через Р_к величину растягивающей силы в момент разрыва, получим:

. (2.1)

Если в процессе растяжения дойти до некоторой точки М, напряжение для которой выше предела упругости, а затем начать разгрузку, то линия разгрузки будет выражаться прямой MN, параллельной начальному участку диаграммы OB. При полном снятии нагрузки в образце сохраняется остаточная деформация l_ост. Полная деформация испытываемого образца состоит из двух частей:

,

где l_упр  упругая деформация, исчезающая после снятия нагрузки; l_ост  остаточная деформация.

После испытания образца определяют относительное остаточное удлинение при разрыве:

,

и относительное остаточное сужение в шейке:

,

где l_К и F_К  длина образца и площадь поперечного сечения в шейке после разрыва. Величины  и  являются характеристиками пластичности материала. Для Ст3  = 2127 %;  = 6070 %.

Разделив нагрузку P на начальную площадь поперечного сечения F₀, а абсолютное удлинение l на расчетную длину образца l₀, получим так называемую диаграмму напряжений в координатах  (рис. 2.3), вид которой совпадает с диаграммой растяжения. Из диаграммы видно, что:

, (Закон Гука)

где Е  модуль продольной упругости (модуль упругости первого рода, модуль Юнга).

Если в ходе испытания измерять поперечную деформацию  и следить за изменением отношения /, то можно обнаружить, что в зоне малых упругих деформаций это отношение останется практически постоянным. Величину называют коэффициентом поперечной деформации или коэффициентом Пуассона. Величины Е и  характеризуют упругие свойства материалов, поэтому их называют упругими постоянными. Для Ст3 Е = 210⁵ МПа;  = 0,3.

Нисходящий участок ЕК диаграммы напряжений носит условный характер, поскольку площадь поперечного сечения образца непрерывно уменьшается после образования шейки. Деля величину силы на действительную площадь поперечного сечения образца F_i, можно построить истинную диаграмму напряжений. Истинное сопротивление в момент разрыва определяется .