1.8 Растяжение и сжатие

Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние силовые факторы равны нулю.

Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными.

Продольные силы определяются с помощью метода сечений.

Пример 1: Пусть имеется ступенчатый стержень, нагруженный силами Р₁ = 2 кН, Р₂ = 3 кН и Р₃ = 2 кН вдоль оси стержня, показанного на рис. 1.14, а. Определить величину продольных сил.

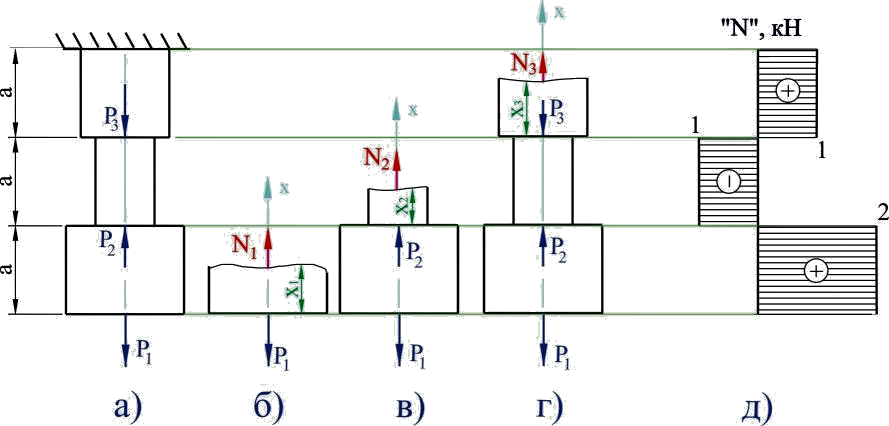
Рисунок 1.14

Решение. Стержень делим на участки по местам приложения нагрузок и по местам изменения поперечного сечения.

Первый участок ограничен точками приложения сил Р₁ и Р₂. Направим ось вдоль оси участка вверх с началом координат в точке приложения силы Р₁ (начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии х₁ от начала первого участка. Причем координата х₁ может быть взята в интервале , где а  длина первого участка.

Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой N₁, предварительно направив ее в сторону растяжения рассматриваемой части.

Из условия равновесия статики:

; , кН

Положительный знак продольной силы говорит о том, что первый участок растянут.

Значение продольной силы не зависит от координаты х₁, поэтому на всем участке значение продольной силы постоянно и равно N₁.

Второй участок ограничен точками приложения сил Р₂ и Р₃. Направим ось х вдоль оси участка вверх с началом координат в точке приложения силы Р₂ (начало второго участка).

Мысленно рассечем второй участок поперечным сечением на расстоянии х₂ от начала второго участка. Причем координата х₂ может быть взята в интервале , где а  длина второго участка.

Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой N₂, предварительно направив ее в сторону растяжения рассматриваемой части.

Из условия равновесия статики:

; , кН

Знак минус говорит о том, что второй участок сжат.

Аналогично для третьего участка:

; , кН

Полученные результаты для большей наглядности удобней представить в виде графика (эпюры N), показывающего изменение продольной силы вдоль оси стержня. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1.14, д). В одну сторону откладываем положительные значения, в другую  отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а внутри эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («N») и через запятую  единицы измерения (кН)

Пример 2: Два стержня, соединенные в т. А, находятся под действием силы Р (рис. 1.15,а). Определить усилия, действующие в стержнях.

а)

б)

в)

Решение.

Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n-n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N₁ и N₂ в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис. 1.15,б).

Уравновесим отсеченную часть, запишем уравнения: .

Решая, из первого уравнения получим:

,

из второго уравнения окончательно имеем:

; .

Так как величина силы N₂ < 0, то её направление следует изменить на противоположное (рис. 1.15,в). Согласно рисунку нормальная сила N₁ растягивает отсеченную часть стержня 1  она положительна, сила N₂ сжимает отсеченную часть стержня 2  она отрицательна.

Пример 3: Абсолютно жесткий брус подвешен на двух стержнях и находится под действием силы Р (рис. 1.16,а). Определить усилия в стержнях.

Используя метод сечений, получим отсеченную часть, показанную на рис. 1.16,б.

Запишем уравнения равновесия: и :

Решая систему уравнений, получим:

; .