12.6 Логарифмический декремент затухания

Натуральный логарифм отношения следующих друг за другом через период амплитуд характеризует темп колебаний и называется логарифмическим декрементом затухания , равным:

. (12.9)

При не слишком быстром процессе затухания, когда уменьшение амплитуды  за цикл значительно меньше самой амплитуды , можно записать:

,

,

(если разложить в ряд и ограничиться, ввиду малости последующих членов, двумя его первыми членами). Тогда:

, (12.10)

Сравнивая (12.9) и (12.10), имеем:

, (12.11)

т.е. логарифмический декремент равен отношению уменьшения амплитуды за один цикл к значению амплитуды этого цикла.

В момент времени, когда перемещение системы достигает максимума, ее полная энергия равна потенциальной энергии:

.

Потеря энергии за один цикл составит:

.

Относительное рассеяние энергии:

(12.12)

называют коэффициентом поглощения. Сравнивая (12.11) и (12.12), видим, что коэффициент поглощения вдвое больше логарифмического декремента. Другими словами, логарифмический декремент равен половине рассеяния энергии за один цикл колебаний.

Измеряя в нескольких местах записи амплитуды затухающих колебаний ₁, _i+1 или потерю энергии за цикл по формулам (12.11) и (12.12), можно найти логарифмический декремент и, следовательно, коэффициент затухания .

12.7 Коэффициент динамичности

Амплитудой вынужденных колебаний определяются максимальные динамические напряжения, возникающие в упругих системах от воздействия на них возмущающих сил. Величина этих напряжений, как и амплитуда , зависит не столько от величины возмущающей силы Р, сколько от частоты ее изменений во времени . При одном и том же значении Р амплитуда и возникающие в системе напряжения могут значительно изменяться в зависимости от изменений частоты .

Для оценки этих изменений их сравнивают со статическим отклонением _ст системы при действии на неё максимального (амплитудного) значения возмущающей силы Р статически. Имея в виду, что g = P / m; ₀² = С / m, находим:

. (12.13)

Отношение амплитуды  к _ст, равное, с учетом (12.13):

, (12.14)

называется коэффициентом нарастания амплитуды, или коэффициентом динамичности. Коэффициент динамичности показывает, во сколько раз амплитуда вынужденных колебаний больше максимального статического отклонения, вызванного максимальным значением возмущающей силы.

Величина  зависит от отношения частот /₀ и коэффициента затухания . Графики зависимости  от /₀ приведены на рис. 12.8. При малой частоте возмущающей силы  близок к единице. С ростом частоты  значение  быстро увеличивается и при  = ₀ достигает очень больших величин:

.

Это значение выражается через логарифмический декремент:

.

Например, для стальных конструкций, имеем: Т = 0,080,09; _рез  3740.

Явление, при котором частота возмущающей силы  совпадает с частотой собственных колебаний системы ₀, а амплитуда вынужденных колебаний становится недопустимо большой, особенно при небольших значениях сил затухания (при   0;   ), называется резонансом.

Заметим, что при   0 коэффициент нарастания амплитуды имеет максимальное значение несколько левее резонанса, т.е. _рез  _max.

Рисунок 12.8

Чтобы убедиться в этом, возьмем производную  по /₀ и приравняем её к нулю:

.

Знаменатель этой дроби не может равняться бесконечности при конечных значениях , ₀, . Следовательно, имеем два условия равенства нулю этой производной:

, или ,

т.е. .

Подставляя это значение /₀ в формулу (12.14), получим максимальную величину динамического коэффициента амплитуды (при   0):

,

т.е. в этом случае коэффициент  выше, чем при резонансе. Лишь при  = 0 коэффициент  имеет максимальное значение при резонансе (  ).

Если частота  больше частоты ₀, то амплитуды становятся конечными; при  = ₀2^0,5 динамический коэффициент становится меньше единицы. При очень больших значениях отношения /₀ динамический коэффициент становится весьма малым. Это означает, что система под действием высокочастотной нагрузки практически не совершает колебаний, т.е. она как бы "не успевает" отзываться на весьма быстрые изменения возмущающей силы. Заметим, что хотя такая нагрузка безопасна для прочности конструкции, она может оказаться очень вредной для обслуживающего персонала. Человеческий организм болезненно реагирует на высокочастотные колебания, если даже их амплитуда мала.

Из рис. 12.8 видно, что при режимах, далеких от резонанса ( < ₀ и  > ₀), затухание мало влияет на величину коэффициента динамичности. Это дает возможность вести расчет таких режимов без учета демпфирования 2/₀, т.е. приближенно полагать:

.

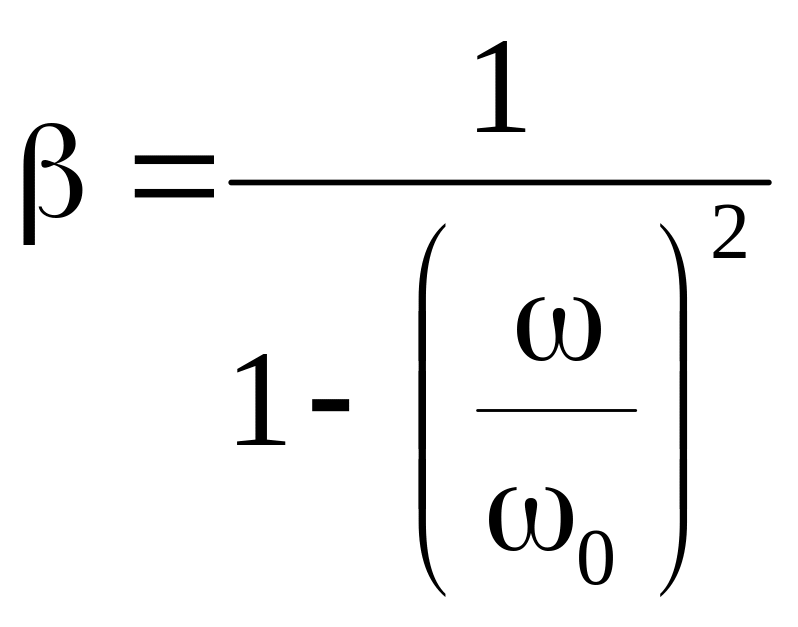Если коэффициент  найден, легко определяются напряжения в упругих элементах колебательной системы:

,

где под _ст понимается напряжение, которое возникло бы в системе при статическом приложении максимального значения возмущающей силы. По напряжению  при необходимости может быть проведен расчет наиболее напряженных элементов на усталостную прочность.

В случае, когда сопоставление частот  и ₀ указывает на опасность резонанса, обычно путем конструктивных изменений добиваются изменения той или иной частоты. Наиболее целесообразным будет изменение частоты в сторону увеличения отношения /₀, с тем чтобы добиться более заметного снижения коэффициента . Этого можно достигнуть, например, уменьшением жесткости упругих элементов колебательной системы либо установкой специальных устройств, повышающих рассеяние энергии при колебаниях. Коэффициент затухания  при этом возрастает, а амплитуда в зоне резонанса при неизменном отношении частот снижается (см. рис. 12.8). Легко увидеть, что:

при  > 1;

при  = 1;

при  < 1.

Критическое значение коэффициента затухания  = 0, 5₀ находят из условия, что при резонансе ( = ₀)  = 1.

При обычных условиях работы оборудования не следует допускать превышения амплитуды вынужденных колебаний статического перемещения более чем вдвое. Иначе говоря, коэффициент нарастания амплитуды  не должен быть выше 2.

При этом, как видно из выражения (12.14), должны быть обеспечены соотношения:

или .

С некоторым запасом область 0,7₀ <  < 1,3₀ считают запретной, хотя быстрый переход через нее вполне возможен, так как нарастание амплитуды требует определенной затраты энергии и времени.