12.2 Жесткость системы (коэффициент упругого сопротивления)

Под жесткостью понимаем обобщенную нагрузку (линейную силу Р или крутящий момент М), вызывающую обобщенную деформацию (соответственно, линейную  или угловую ) в данной точке, равную единице. Очевидно, что полная деформация ( или ) может быть определена путем деления действующей на систему нагрузки Р или М на ее жесткость С:

; . (12.1)

С другой стороны, деформация системы может быть определена методами сопротивления материалов. Так, например, деформация изображенного на рис. 12.3 стержня в соответствии с законом Гука будет равна:

. (12.2)

Из выражений (12.1) и (12.2) имеем жесткость стержня при растяжении, равную:

.

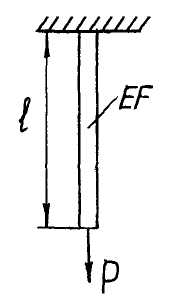
Рисунок 12.3

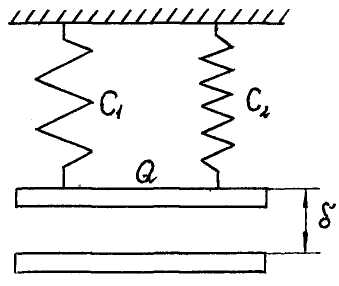
Рисунок 12.4

12.3 Жесткость системы при параллельном соединении упругих

элементов

Пусть жесткая балка весом Q подвешена на пружинах жесткостью С₁ и С₂ (рис. 12.4). Очевидно, всегда можно так подвесить балку и распределить её вес по пружинам, что каждая из пружин растянется на одну и ту же величину . Обозначим часть веса балки, приходящуюся на каждую из пружин, соответственно, Q₁ и Q₂. Очевидно, что Q = Q₁ + Q₂. Заменив в соответствии с формулой (12.1) Q = C; Q₁ = С₁ и Q₂ = С₂, имеем:

,

или

.

Следовательно, при параллельном соединении упругих элементов жесткость системы равна сумме жесткостей упругих элементов, ее составляющих:

.

12.4 Жесткость системы при последовательном соединении упругих

элементов

При последовательном соединении пружин (рис. 12.5) на каждую из них действует вес груза Q. Очевидно, что:

,

или, в соответствии с формулой (12.1):

; .

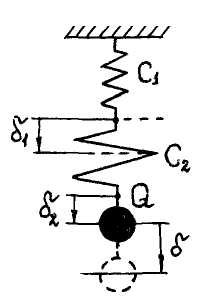
Рисунок 12.5

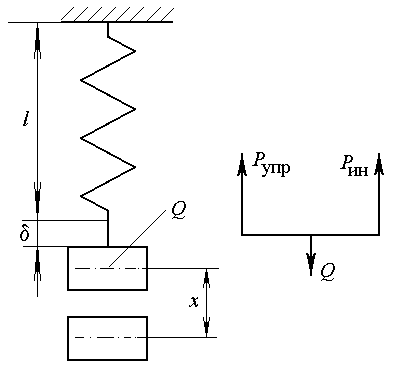
Рисунок 12.6

Окончательно имеем:

.

Таким образом, при последовательном соединении упругих элементов величина, обратная жесткости системы, равна сумме величин, обратных жесткости упругих элементов, ее составляющих.

12.5 Свободные колебания систем с одной степенью свободы.

Колебания без затухания

В данном случае и в дальнейшем ограничимся рассмотрением таких колебаний, для которых справедлив закон Гука и принцип независимости действия сил.

Рассмотрим простейшую систему, состоящую из груза, подвешенного на вертикально расположенной пружине (рис. 12.6). Влиянием собственного веса пружин пренебрегаем. Направим ось x вдоль оси пружины вниз.

За начало отсчета 0 возьмем положение статического равновесия груза Q.

В этом положении пружина растянута на величину  = Q/C, где С  жесткость пружины. Рассмотрим движение груза в произвольный момент времени t. Отклонение центра массы груза в этот момент от положения статического равновесия вниз обозначим через х. Получаем:

; ; .

При составлении уравнения движения будем исходить из принципа Даламбера, который заключается в том, что к движущейся с ускорением системе применимы соотношения статики при условии, что в число внешних сил включена фиктивная сила инерции, равная произведению массы на ускорение и направленная против ускорения. Полагаем, что скорость dx/dt и ускорение d²x/dt² совпадают по направлению с отклонением X. При отклонении груза возникает упругая сила Р_упр которая стремится вернуть груз в состояние равновесия и потому называется восстанавливающей силой.

Дифференциальное уравнение колебаний получим, спроектировав все действующие силы на вертикальную ось:

.

Отсюда имеем:

, (12.3)

Или

, (12.4)

где .

Решением уравнения (12.3) будет:

. (12.5)

где А и В  постоянные интегрирования, зависящие от начальных условий, т.е. от положения груза m = Q / g и его скорости dx/dt в момент времени t = 0.

Если заданы начальная координата груза х₀ и начальная скорость ₀, то из (12.5) определим:

; .

Полагая

и , (12.6)

решение (12.5) можно представить в виде:

. (12.7)

или

,

где   амплитуда колебаний, определяемая формулой:

.

Величина ₀t +  называется фазой колебаний, а величина   сдвигом фазы. На основании (12.7)  может быть определена из условия tg = х₀₀/₀.

Уравнение (12.7) выражает процесс чисто периодического собственного колебания системы. График его представлен на рис. 12.7.

Период колебаний Т определяется из условия, что при увеличении времени t на величину Т аргумент, стоящий под знаком синуса, изменится на 2:

.

Период представляет собой время, в течение которого совершается одно колебание. Если Т  время одного колебания, то в 2 секунд будет происходить ₀ колебаний. Поэтому величина ₀ и носит название круговой частоты (в отличие от секундной частоты f = 1/Т):

.

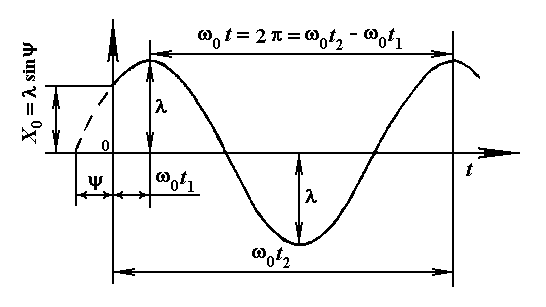
Рисунок 12.7

Круговую частоту часто называют частотой собственных колебаний системы, поскольку она, как это видно из (12.4), зависит не от начальных обстоятельств колебательного процесса, а от величины колеблющейся массы и жесткости системы. Формуле (12.4) можно придать вид:

, (12.8)

где g  ускорение свободного падения, м/с²; _с  статическое удлинение пружины под действием груза Q.