Вопросы для самопроверки

1. Назовите основные причины, вызывающие появление динамических нагрузок.

2. Как найти деформацию возникающую во вращающемся кольце?

3. Что такое динамический коэффициент?

4. Как определяются механические свойства материалов при ударе?

5. В чем заключается явление усталости материала?

6. Проанализируйте влияние конструктивно-технологических факторов на предел усталости материала.

Лекция 12 Расчет на прочность при колебаниях

Основные понятия; жесткость системы (коэффициент упругого сопротивления); жесткость системы при параллельном и последовательном соединении упругих элементов; свободные колебания систем с одной степенью свободы; колебания без затухания; логарифмический декремент затухания; коэффициент динамичности

12.1 Основные понятия

Колебательным называется процесс, при котором физической величине, его характеризующей, свойственны переходы от возрастания к убыванию, чередующиеся с переходами от убывания к возрастанию. Если колебания представляют собой механическое движение (перемещение какого-либо тела), то происходит механический колебательный процесс  механические колебания.

Колебания различают:

1. В зависимости от наличия динамических сил колебания подразделяют на собственные (свободные) и вынужденные.

Собственными называются колебания, возникающие в системе вследствие внешнего кратковременного начального воздействия (толчка) и совершающиеся затем благодаря действию внутренних упругих сил, без притока энергии извне. За счет сил сопротивления (трения среды, вязкости материала) эти колебания постепенно затухают, и через некоторое время система приходит в свое исходное состояние.

Вынужденными называются колебания упругой системы, происходящие под действием внешних возмущающих сил, периодически изменяющихся по любому закону.

2. По виду деформаций упругих элементов конструкций:

-

Рисунок 12.1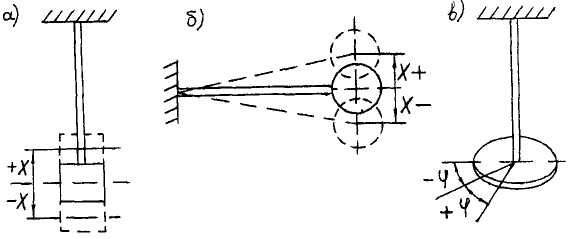

на продольные, сопровождаемые деформациями растяжения  сжатия (рис. 12.1, а);

- поперечные (изгибные), сопровождаемые деформациями изгиба (рис. 12.1, б);

- крутильные, сопровождаемые деформациями кручения (рис. 12.1, в).

Часто приходится иметь дело со смешанными изгибно-крутильными колебаниями.

3. По числу степеней свободы различают системы с одной, многими и бесчисленным количеством степеней свободы.

Числом степеней свободы упругой системы называется число независимых координат, определяющих положение всех масс системы в любой момент времени.

Известно, что перемещение материальной точки может быть разложено по осям координат на три линейных перемещения. В этом случае говорят, что материальная точка имеет три степени свободы. Механическую систему можно рассматривать как состоящую из бесконечного множества материальных точек. С этой точки зрения любая упругая система имеет бесконечное число степеней свободы. Однако при решении практических задач пользуются упрощенными расчетными схемами.

Во всех случаях, когда система состоит из упругих элементов (стержней, пружин, валов и т.п.), несущих массивные грузы, влиянием массы упругих элементов пренебрегают. В других случаях эту массу "приводят" в точки приложения нагрузок.

Расчетная схема системы, таким образом, представляется в виде упругих невесомых элементов с закрепленными в отдельных точках сосредоточенными массами. Число степеней свободы такой системы будет определяться количеством колеблющихся масс и возможностями их перемещения. На рис. 12.2а представлена система, имеющая одну степень свободы, так как положение груза определяется одной координатой х  перемещением по вертикали; на рис. 12.2б, в  системы с двумя степенями свободы, так как положение грузов характеризуется двумя координатами. Увеличивая число сосредоточенных масс колеблющейся балки, переходим в пределе к балке с распределенной по всей длине массой  к колебательной системе (рис. 12.2г) с бесконечным числом степеней свободы.

4

Рисунок 12.2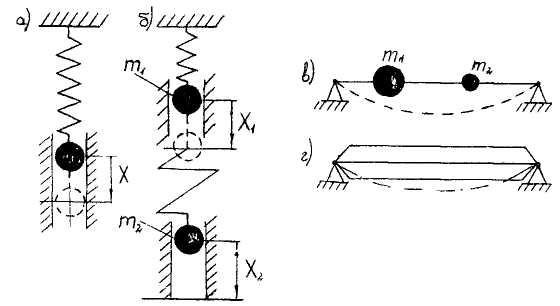

. По виду функций отклонений при колебаниях различают периодические и непериодические колебания. Периодическими колебания называются в том случае, если каждое значение отклонения повторяется неограниченное количество раз через равные промежутки времени, называемые периодами.

5. В зависимости от учета сил сопротивления имеем затухающие и незатухающие колебания.

Если восстанавливающая сила при колебании линейно зависит от отклонений, имеем линейные колебания. В противном случае возникают нелинейные колебания.