11.3 Механические свойства материалов при ударе

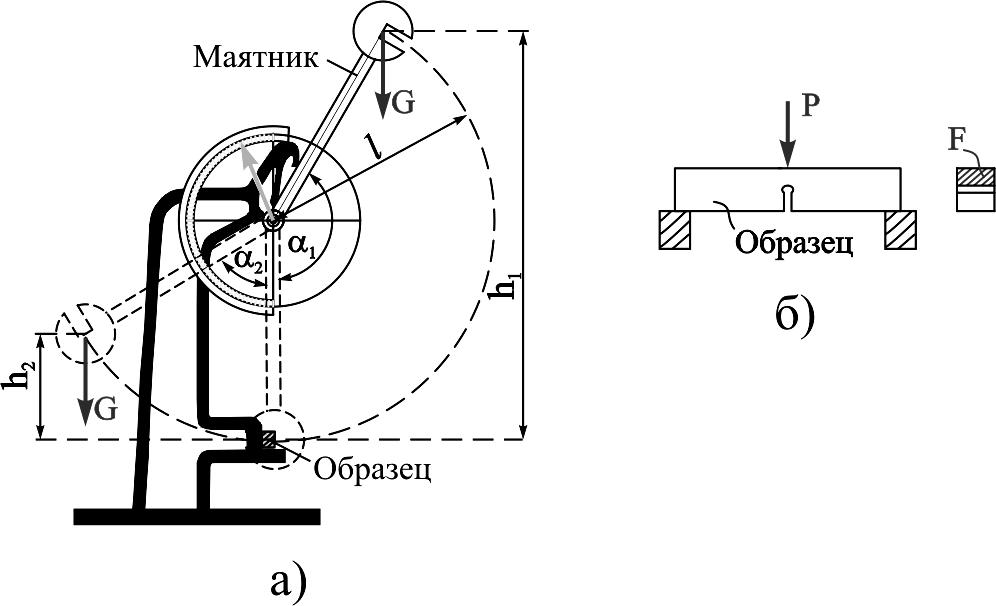
Для проверки способности материала сопротивляться ударным нагрузкам проводят испытания ударным изгибом – определение ударной вязкости надрезанных образцов. Эти испытания проводят на маятниковых копрах (рис. 11.3, а). На рис. 11.3, б показан применяемый при испытании образец. Разность высот маятника до и после удара позволяет вычислить работу А, израсходованную на разрушение образца.

Ударной вязкостью материала называется величина работы разрушения образца, отнесенная к площади поперечного сечения в месте надреза F:

Рисунок 11.3

. (11.18)

Данные об ударной вязкости не могут быть использованы при расчете на прочность, но они позволяют оценить особое качество металла – его склонность к хрупкости при динамических нагрузках. Низкая ударная вязкость служит основанием для браковки материала. Стали, применяемые для изготовления деталей, работающих при динамических нагрузках, должны иметь ударную вязкость не менее  Дж/м².

11.4 Напряжения, изменяющиеся во времени. Явление усталости материалов

М

Рисунок 11.4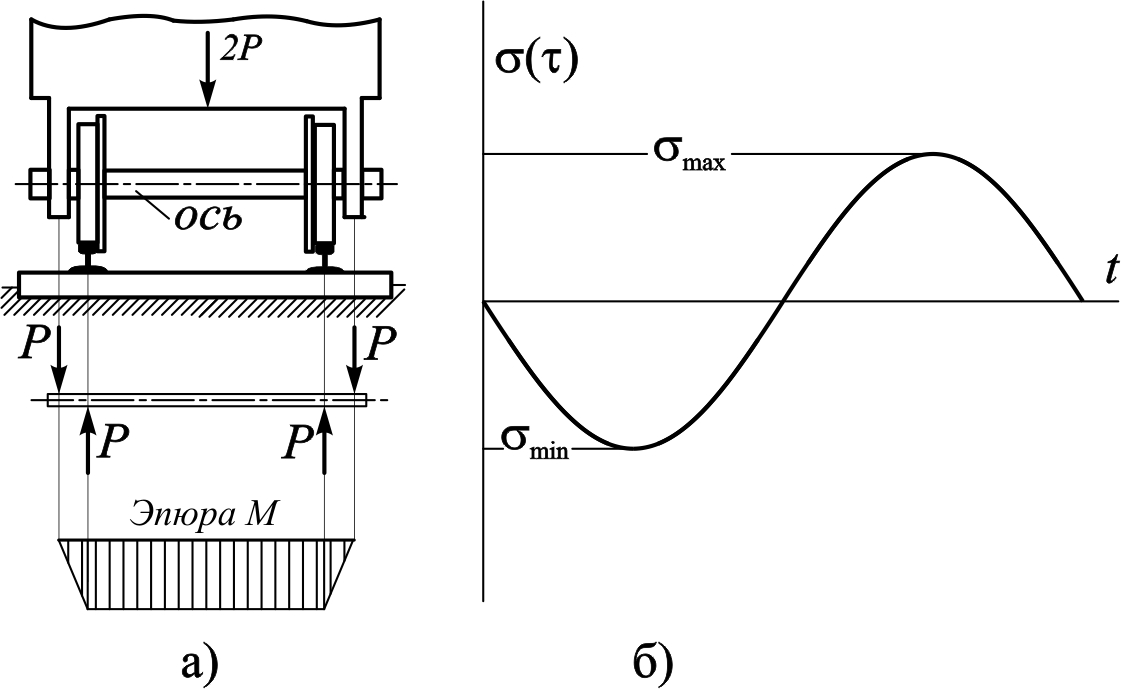

ногие детали машин работают при переменных во времени нагрузках и, следовательно, возникающие в них напряжения также переменны во времени. Практика машиностроения уже в середине XIX века показала, что это обстоятельство необходимо учитывать. Особенно наглядно влияние переменности напряжений на прочность выявили железнодорожные катастрофы, вызванные поломками осей вагонов. Эти оси, рассчитанные по статическим механическим характеристикам σ_т или σ_в, разрушались, проработав некоторое время в условиях переменных напряжений, вызванных вращением оси относительно вагона и ударными нагрузками из-за неправильностей рельсового пути.

Вагонная ось неподвижного состава (рис. 11.4, а) нагружена таким образом, что в верхней части поперечного сечения возникают нормальные напряжения растяжения, а в нижней – сжатия. При движении вагона каждая точка оси оказывается то в верхней части, то в нижней половине сечения; напряжения изменяются по синусоиде (рис11.4, б).

Законы изменения нагрузок во времени могут быть самыми разнообразными. Далее мы рассмотрим только простейшие режимы, которые вызывают в деталях циклически изменяющиеся во времени напряжения. К таким режимам сводится или может быть сведено нагружение большинства деталей машин и элементов конструкций.

Обычно предполагают, что закон изменения напряжений характеризуется кривой имеющей вид синусоиды (рис. 11.5). Как показывают многочисленные эксперименты, вид этой кривой не имеет значения; прочность материала зависит от величин наибольшего и наименьшего напряжений.

Совокупность всех последовательных значений переменных напряжений за один период их изменения называется циклом напряжений.

Наибольшее (в алгебраическом смысле) напряжение цикла называется максимальным _max, а наименьшее – минимальным _min.

Алгебраическая полусумма максимального и минимального напряжения цикла называется его средним значением:

Рисунок 11.5

. (11.19)

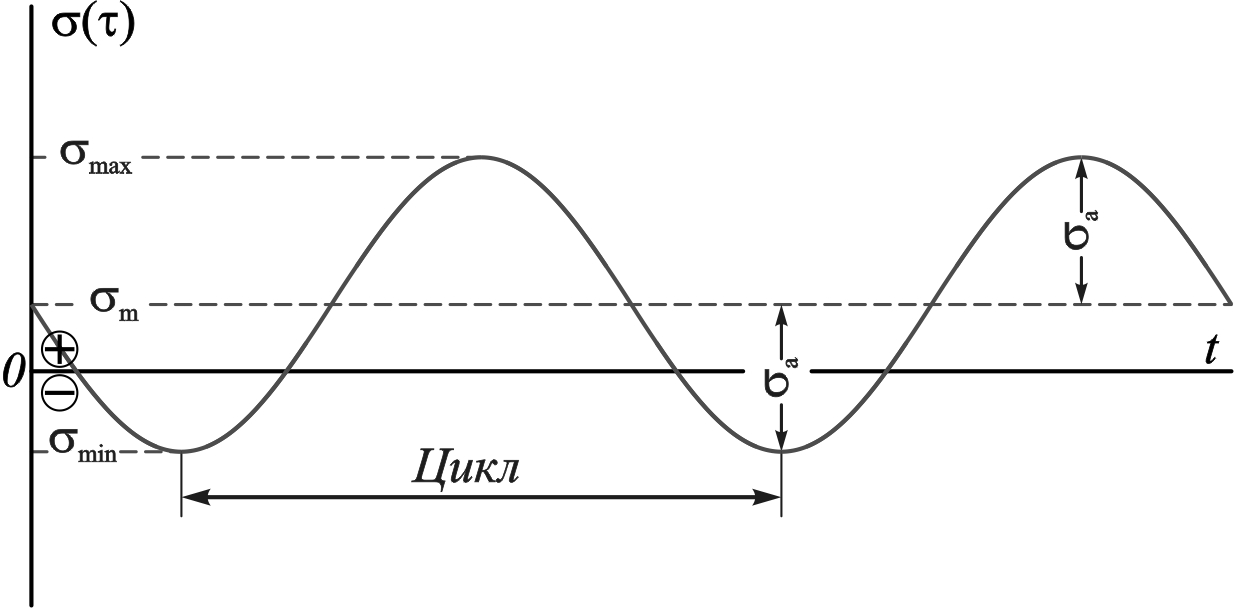
Алгебраическая полуразность максимального и минимального напряжений называется амплитудой цикла:

. (11.20)

Важной характеристикой цикла напряжений является коэффициент асимметрии цикла:

.

Для статического нагружения _max = _min (рис. 11.6), поэтому R = 1.

Если напряжения _max = _min = _a, то цикл называют симметричным.

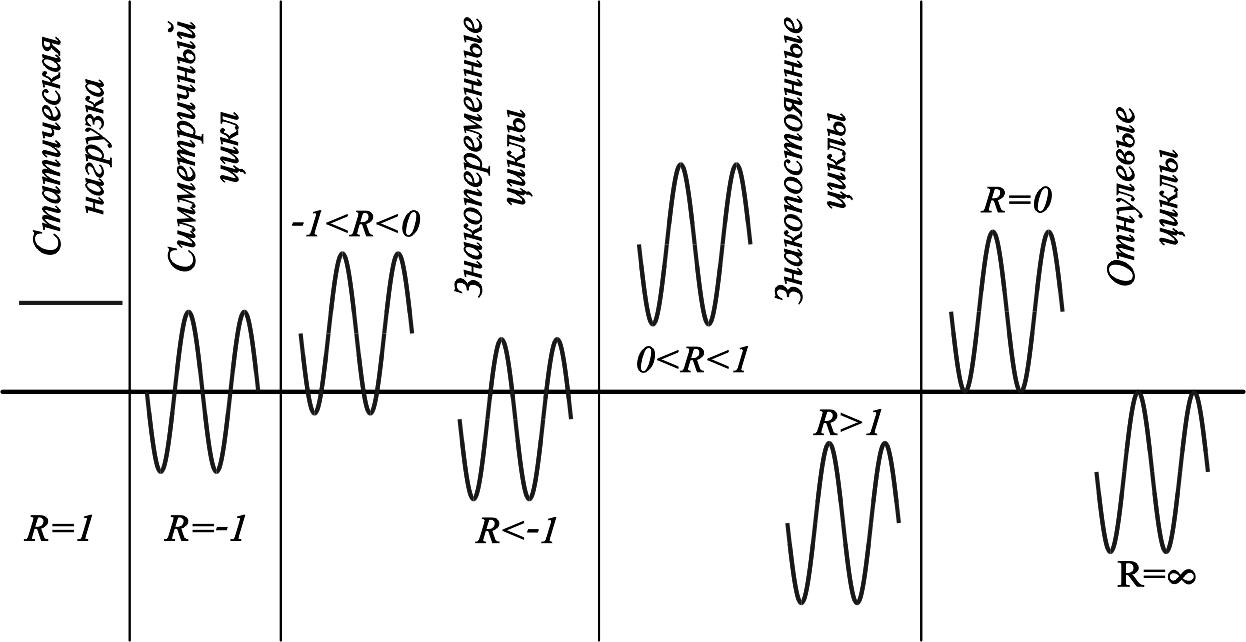
Рисунок 11.6

Ассиметричные циклы могут быть знакопеременными, знакопостоянными и отнулевыми (пульсирующими).

Многократные опыты позволили установить, что при действии переменных напряжений разрушение материалов происходит при напряжениях _max и _min, значительно меньших, чем опасные напряжения при статическом нагружении. Другими словами, многократное приложение нагрузки приводит к понижению прочности. Такое явление называется усталостью.

Причиной разрушения при циклических нагрузках является неоднородность структуры металла (наличие зерен, микроскопических трещин и т.п.).

При действии повторных повторяющихся напряжений в окрестностях точек с пониженной прочностью возникают микроскопические трещины. У концов этих трещин возникает высокая концентрация напряжений, приводящая к развитию трещин по мере увеличения числа циклов. Если площадь сечения в результате развития трещин уменьшится на столько, что сечение не выдерживает возникающего в нем усилия, происходит разрушение элемента. Получается, что явление усталости материала заключается в постепенном накоплении повреждений материала при действии повторно-переменных напряжений, приводящих к образованию трещин и разрушению.

Например, для того чтобы сломать проволоку, мы перегибаем ее несколько раз то в одну, то в другую сторону. При этом в продольных волокнах проволоки создаются попеременно то растягивающие, то сжимающие напряжения. Если проволоку перегибать сильно, то она сломается после 510 циклов. Не трудно убедиться, что если уменьшить степень перегиба, то число циклов до разрушения увеличится. Перегибая проволоку, мы стремимся создать в ней пластическую деформацию. Если этого не делать, то максимальные напряжения окажутся меньше предела текучести и проволока может выдержать миллионы циклов.

П

Рисунок 11.7

ри переменных напряжениях поверхности развивающихся трещин многократно трутся друг о друга, в результате чего они шлифуются. Поэтому поверхность излома при усталостном нагружении состоит из двух зон (рис. 11.7, а): одна из них (зона А) имеет нормальную для металла зернистую структуру, а другая (зона Б) имеет шлифованную поверхность.

На рисунке 11.7, б приведена фрактография образца круглого поперечного сечения после испытания его на усталость при поперечном изгибе. Здесь четко различимы две характерные зоны: зона (Б) роста трещин и зона (А) окончательного излома.