10.5 Расчеты на устойчивость при помощи коэффициентов уменьшения основного допускаемого напряжения

Очевидно, что при практических расчетах на устойчивость стержня нельзя допускать возникновения в нем критического напряжения, а следует принять соответствующий запас устойчивости. Если принять определенное значение коэффициента запаса на устойчивость n_у, то допускаемое напряжение на устойчивость []_у можно определить следующим образом:

. (10.9)

Коэффициент запаса на устойчивость для сталей выбирают в пределах 1,73,0; для чугуна – в пределах 5,05,5; для дерева – 2,83,2. Причем, меньшие значения принимают при большей гибкости.

10.6 Рациональные формы сечений стержней

Величина критических напряжений, определяемых по формуле Эйлера, обратно пропорциональна гибкости стержня:

Стержни одинаковых длин и способах закрепления могут иметь разные гибкости в зависимости от их форм поперечного сечения. Вычисляя радиус инерции сечения i_min или относительный радиус инерции , можно провести сравнительную оценку форм поперечных сечений стержней на способность сопротивляться потери устойчивости, так как чем больше _min,тем больше величина критической силы тем устойчивее стержень. Очевидно, что наиболее устойчивыми являются стержни с кольцевой или коробчатой формами поперечных сечений.

Вопросы для самопроверки

Опишите явление потери устойчивости.
Какая механическая система называется устойчивой и неустойчивой?
Приведите примеры устойчивых и неустойчивых объектов.
Что означает выражение «сжатый стержень потерял устойчивость»?
Какая сила называется критической?
Почему в реальных конструкциях сжимающие стержень силы должны быть меньше критических?
Почему нельзя допускать потерю устойчивости элементов конструкций?
Запишите формулу Эйлера.
Как влияют условия закрепления стержня на величину критической силы?
Сформулируйте условие применимости формулы Эйлера.
Запишите формулу Ясинского.
Могут ли быть такие случаи, когда сжатый стержень не будет терять устойчивость?
Нарисуйте график зависимости _кр = f().
Опишите в общем виде схему расчета сжатых стержней с помощью коэффициента уменьшения допускаемого напряжения.

Лекция 11 Динамическое нагружение

Понятие о динамическом действии нагрузки; удар; механические свойства материалов при ударе; напряжения, изменяющиеся во времени; явление усталости материалов; влияние конструктивно-технологических факторов на предел усталости; практические меры повышения сопротивления усталости

11.1 Понятие о динамическом действии нагрузки

Ранее во всех рассмотренных нами задачах предполагалось, что действующие нагрузки статические, т.е. не изменяющиеся с течением времени. При проектировании машин обычно сталкиваются с деталями, находящимися в неравномерном движении, что приводит к появлению инерционных нагрузок.

Примером статической нагрузки, или статического действия нагрузки, может послужить действие подвешенного на цепи груза. Это действие остается статическим, если груз будет подниматься цепью с постоянной скоростью. Но тот же груз, поднимаемый цепью с ускорением, будет действовать на цепь динамически. Для расчета цепи в данном случае мы должны учесть не только вес груза, но и силу инерции груза.

Рисунок 11.1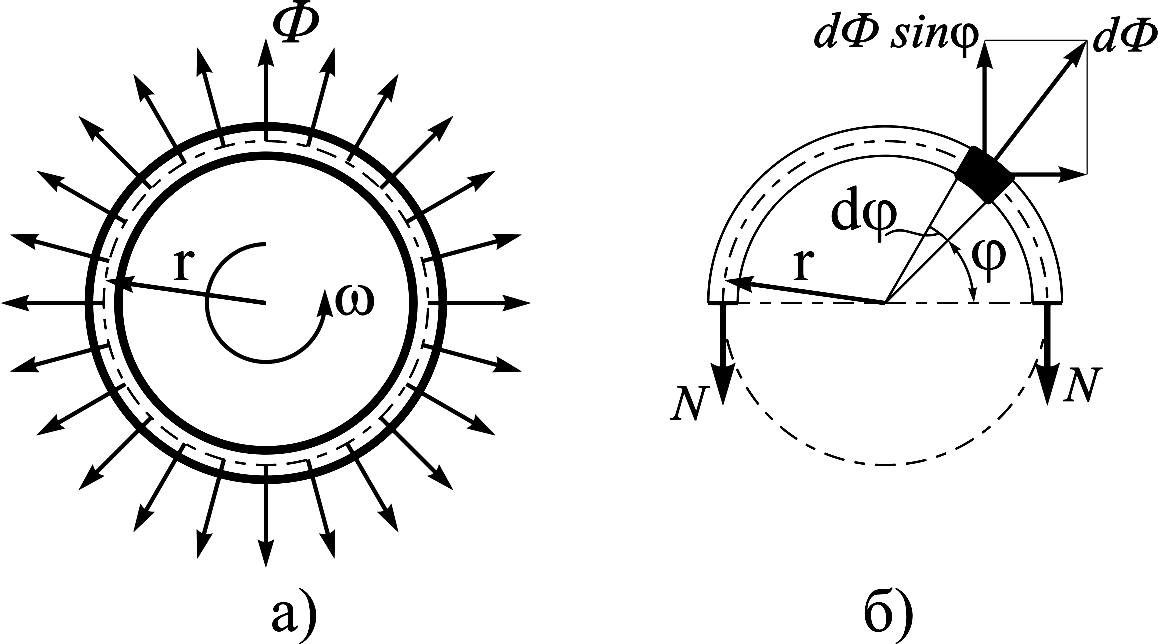

ля примера рассмотрим расчет равномерно вращающегося тонкого кольца (рис. 11.1, a).

Для расчета примем следующие обозначения: r  средний радиус кольца; F  площадь поперечного сечения;   удельный вес материала;   угловая скорость кольца; g  ускорение силы тяжести.

Рассмотрим бесконечно малый элемент кольца массой dm, вырезанный двумя плоскостями, составляющими центральный угол d (рис. 11.1, б)

Элементарная сила инерции dФ:

. (11.1)

Элементарная масса, выраженная через площадь сечения кольца:

. (11.2)

Элементарная сила инерции с учетом (11.2) будет равна:

. (11.3)

Для определения продольной силы N в поперечном сечении кольца рассмотрим равновесие половины кольца под действием двух продольных сил N и суммы вертикальных составляющих элементарных сил инерций: