Вопросы для самопроверки

1. Какой изгиб называется косым?

2. По каким формулам определяются нормальные напряжения в поперечных сечениях балки при косом изгибе?

3. Как находится положение нейтральной оси при косом изгибе?

4. Как определяются опасные точки в сечении при косом изгибе?

5. Как определяются перемещения точек оси балки при косом изгибе?

6. Какой вид сложного сопротивления называется внецентренным растяжением (или сжатием)?

7. По каким формулам определяются нормальные напряжения в поперечных сечениях стержня при внецентренном растяжении и сжатии? Какой вид имеет эпюра этих напряжений?

8. Как определяется положение нейтральной оси при внецентренном растяжении и сжатии? Запишите соответствующие формулы.

9. Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?

10. Как находятся опасные сечения бруса круглого сечения при изгибе с кручением?

11. Какие точки круглого поперечного сечения являются опасными при изгибе с кручением? Какое напряженное состояние возникает в этих точках?

Лекция 10 Устойчивость сжатых стержней: Продольный изгиб

Устойчивое и неустойчивое упругое равновесие; формула Эйлера; влияние способов закрепления концов стержня на критическую силу; пределы применимости формулы Эйлера; расчеты устойчивость при помощи коэффициентов уменьшения основного допускаемого напряжения; рациональные формы сечений стержней

10.1 Устойчивое и неустойчивое упругое равновесие

Д

Рисунок 10.1

о 2-й половины 19 века единственным критерием прочности инженерных сооружений принималась величина действующих напряжений, т.е. считалось, что если напряжения не превосходят некоторого предела, зависящего от механических свойств материала, то сооружению не грозит опасность. С появлением конструкций, в состав которых входят длинные сжатые стержни, последовал ряд аварий, заставивших пересмотреть укоренившуюся точку зрения. Оказалось, что они произошли вследствие недостаточной устойчивости конструкции. Так, например, в результате потери устойчивости под воздействием порывов ветра в 1940 г. в США рухнул Такомский висячий мост (рис 10.1). Тогда погибли 250 человек.

Так при сжатии достаточно длинных и тонких стержней вместо укорочения в соответствии с законом Гука они могут изогнуться (рис. 10.2,а). При прямом изгибе балок направление прогиба балки может существенно отклониться от линии действия нагрузки (рис. 10.2,б), и, наконец, при действии внутреннего давления на цилиндрическую оболочку ее деформации в некоторый момент перестают быть осесимметричными, оболочка искривляется и принимает некоторую новую форму (рис. 10.2,в).

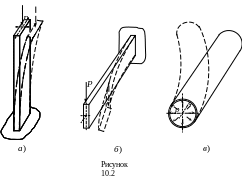
Физическим признаком устойчивости или неустойчивости формы равновесия служит поведение нагруженной упругой системы при её отклонении от рассматриваемого положения равновесия на некоторую малую величину. Если система, отклоненная от положения равновесия, возвращается в первоначальное положение после устранения причины, вызвавшей отклонение, то равновесие устойчиво. Если отклонение не исчезает, а продолжает расти, то равновесие неустойчиво  это явление было названо потерей устойчивости. Нагрузка, при которой устойчивое равновесие переходит в неустойчивое, называется критической нагрузкой, а состояние системы – критическим состоянием.

Эти три формы равновесия можно проиллюстрировать примером из механики твердого тела (рис. 10.3). Будем вкатывать цилиндр на наклонную плоскость ab, которая потом переходит в короткую горизонтальную площадку bc и наклонную плоскость обратного направления cd.

П

Рисунок 10.3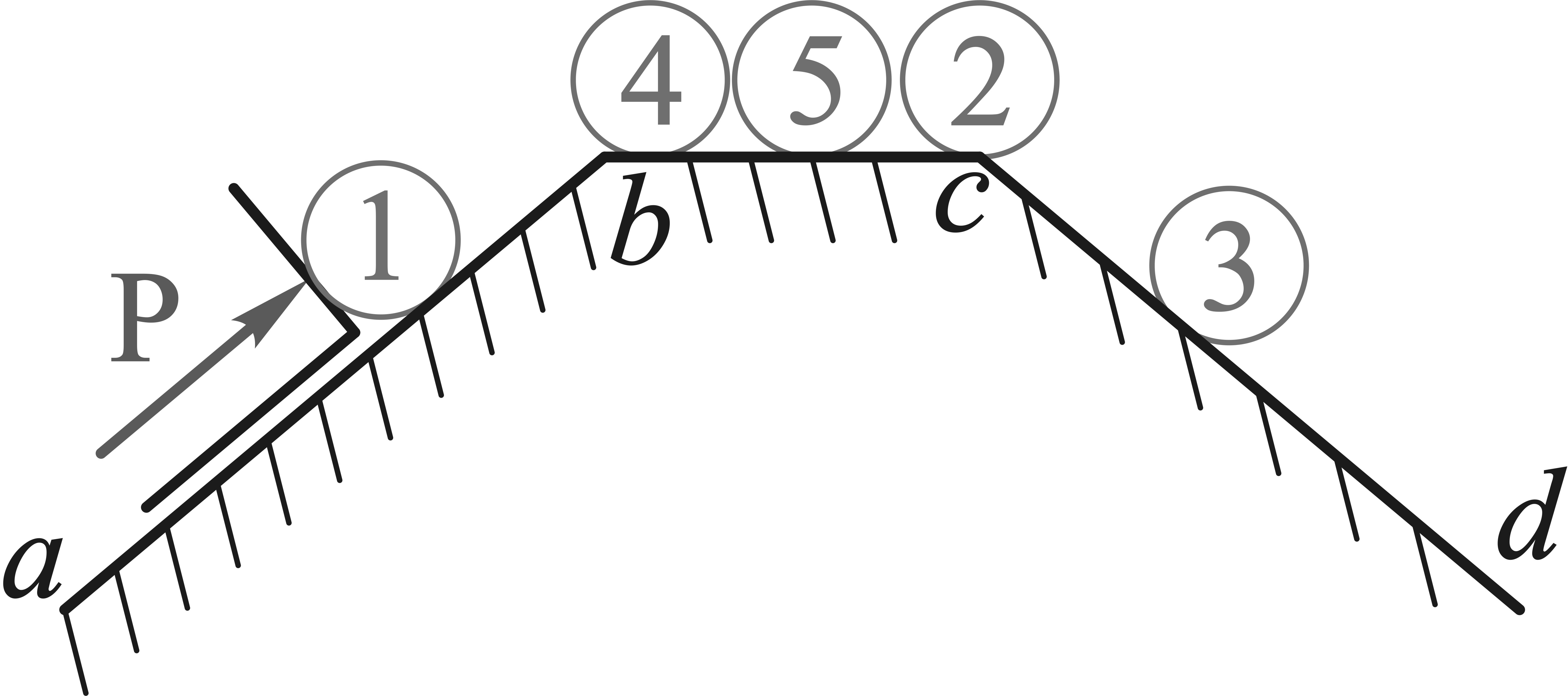

ока мы поднимаем цилиндр по плоскости ab, поддерживая его при помощи упора, цилиндр будет находиться в состоянии устойчивого равновесия. При малых отклонениях цилиндра от положения 1, он будет стремиться вернуться в первоначальное положение. Стоит нам поместить цилиндр в точку с (положение 2), как его равновесие станет неустойчивым – при малейшем отклонении вправо цилиндр начнет двигаться вниз (положение 3); отклонение не исчезает, а продолжает расти.

Между устойчивым и неустойчивым равновесием существует переходное состояние – безразличное (площадка bc). При любом малом отклонении от равновесного состояния 4 цилиндр принимает новое равновесное состояние 5.

Опасность потери устойчивости наглядно можно представить на примере продольного сжатия деревянной линейки. При приложении определенной осевой сжимающей нагрузки, которая при расчете на чистое сжатие не должна привести к разрушению, в действительности происходит разрушение линейки. Причиной разрушения линейки стало то, что при определенной нагрузке линейка потеряла возможность сохранять прямолинейную форму и искривилась, что вызвало появление в поперечном сечении изгибающих моментов, и как следствие, добавочные напряжения от изгиба; линейка потеряла устойчивость.

Поэтому для надежной конструкции мало выполнения рассмотренных ранее условий прочности, так же необходимо, что бы все ее элементы были устойчивы.

Ознакомимся с условиями, при которых устойчивость прямолинейной формы сжатого стержня нарушается. Для этого возьмем достаточно длинный по сравнению с его поперечными сечениями стержень, шарнирно прикрепленный к опорам (рис. 10.4, а) и нагрузим его центральной осевой силой Р.

Рисунок 10.4

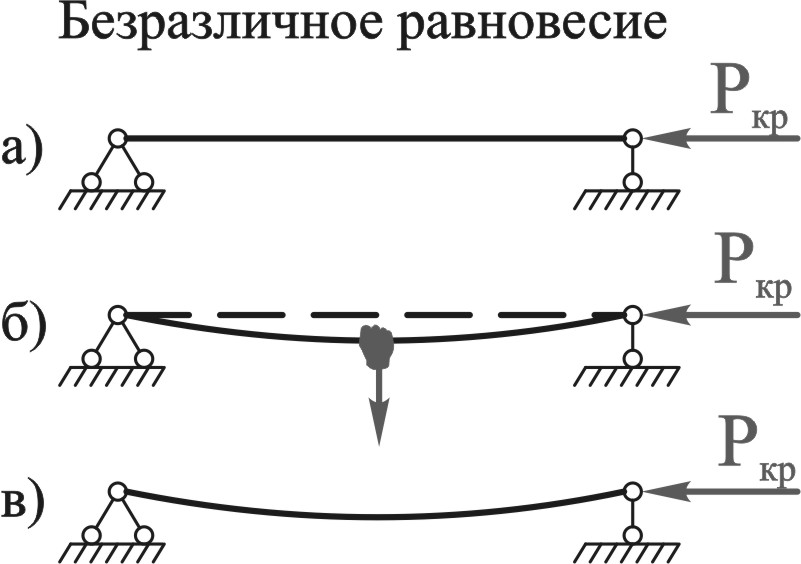
Рисунок 10.5

При попытках отклонить стержень в сторону, например, кратковременным приложением поперечной силы (рис. 10.4, б), он после удаления добавочной силы будет возвращаться к первоначальной прямолинейной форме (рис. 10.4, в).

При возрастании силы Р стержень все медленней будет возвращаться к первоначальной прямолинейной форме.

При некотором значении нагрузки Р_кр, называемом критическим, стержень после небольшого отклонения его в сторону (рис. 10.5, б) уже не выпрямиться, а сохранит вновь приданную форму (рис. 10.5, в).

Таким образом, при критическом значении сжимающей силы стержень будет находиться в безразличном состоянии.

Превышение критической силы, очевидно, произведет к неустойчивому равновесию прямолинейной формы.

Потерю устойчивости прямолинейной формы сжатого стержня иногда называют «продольным изгибом», так как она влечет за собой значительное искривление стержня под действием продольных сил. Для проверки на устойчивость до сих пор сохранился термин «проверка на продольный изгиб», но здесь речь идет не о проверке на изгиб, а о проверке на устойчивость прямолинейной формы стержня.