9.3 Изгиб с кручением

Когда в поперечном сечении бруса равен нулю только один внутренний силовой фактор – продольная сила N, такой вид деформации называют изгибом с кручением.

Изгибу с кручением подвергаются валы различных видов механических передач (ременные, зубчатые и т.д.).

Например, воздействие ролика звена цепи на зуб шестерни цепной передачи (рис. 9.5) будет способствовать возникновению в произвольном поперечном сечении вала пяти внутренних силовых факторов: Q_y, Q_x, Q_z, M_y, M_z, M_кр. В данном случае можно сказать, что вал испытывает деформацию изгиба с кручением.

П

Рисунок 9.5

ри изгибе с кручением в поперечном сечении возникают нормальные напряжения от изгиба в двух плоскостях, а так же касательные напряжения от кручения и изгиба.

Для расчета вала в первую очередь необходимо установить опасные сечения. Для этого строят эпюры изгибающих моментов и крутящего момента, предварительно разложив нагрузки на составляющие вдоль координатных осей (рис. 9.6).

И

Рисунок 9.6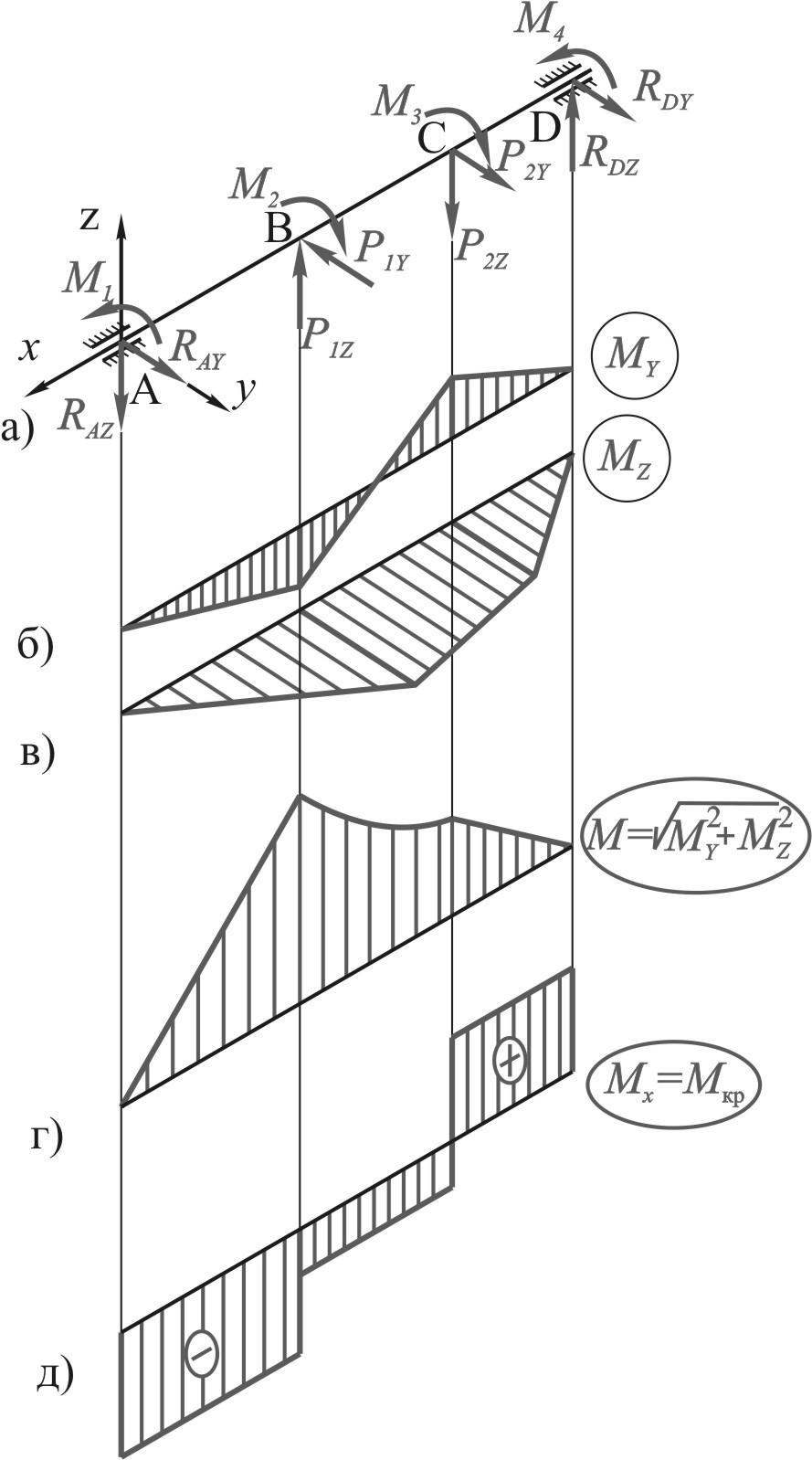

згиб вала круглого и кольцевого поперечного сечения под действием изгибающих моментов M_y и M_z можно привести к прямому изгибу под действием результирующего (суммарного) изгибающего момента (рис. 9.7, а):

(9.9)

Вектор момента М в разных сечениях может иметь различные направления, в силу чего даже при отсутствии распределенных нагрузок эпюра М может быть криволинейной. Но при построении эпюры М обычно несколько завышают значения суммарного изгибающего момента, делая данные эпюры прямолинейными. Вычисляются значения суммарных моментов лишь для тех сечений, где на эпюрах M_y и (или) M_z есть переломы. Эти величины откладывают в масштабе по одну сторону от оси на эпюре М и соединяют прямой линией.

После построений эпюр суммарных изгибающих моментов и крутящих моментов определяют опасное сечение.

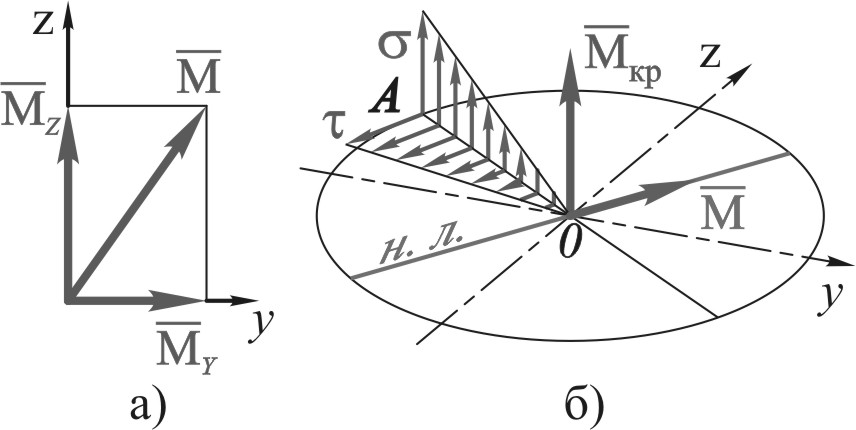
Опасной точкой в сечении вала круглого или кольцевого поперечного сечения, очевидно, будет точка, наиболее удаленная от центра сечения (рис. 9.7, б). В данной точке одновременно и нормальное напряжение от изгиба и касательное напряжение от кручения имеет наибольшее значение:

Рисунок 9.7

;

.

У наиболее опасной точки выделим элемент (рис. 9.8, а). По четырем граням данного элемента действуют касательные напряжения, а к двум из этих граней приложены еще и нормальные напряжения. Остальные две грани свободны от напряжения. Таким образом, при изгибе с кручением элемент в опасной точке находится в плоском напряженном состоянии (рис. 9.8, б).

Заметим, что в данном случае сложного напряженного состояния влиянием касательных напряжений от поперечных сил пренебрегаем, так как они значительно меньше касательных напряжений, вызванных кручением.

Д

Рисунок 9.8

ля проверки прочности элемента, выделенного у опасной точки, нужно, выбрав соответствующую теорию прочности, сравнить значение эквивалентного напряжения с допускаемым для данного материала. Например, по четвертой теории прочности:

, (9.10)

или, учитывая :

. (9.11)

Выражение в числителе представляет собой приведенный момент, действие которого эквивалентно совместному действию трех моментов (согласно принятой теории прочности):

. (9.12)

Теперь условие прочности можно заменить простой формулой:

. (9.13)

При проектировочном расчете валов круглого поперечного сечения пользуются зависимостью полученной из условия прочности (9.13):

. (9.14)