7.6. Перемещения при плоском изгибе

При изгибе рассматриваются перемещения: прогиб и угол поворота поперечного сечения.

Прогибом балки  называется величина, на которую перемещается центр тяжести поперечного сечения в направлении, перпендикулярном первоначальной оси балки. Углом поворота поперечного сечения q называется угол, на который поворачивается поперечное сечение при деформации балки (рис. 7.5).

В дальнейшем будем считать, что прогибы и углы поворота балки малы и , а .

Приближенное дифференциальное уравнение изогнутой оси балки имеет вид: .

Если балка имеет один участок, то это уравнение можно непосредственно проинтегрировать:

, (7.10)

, (7.11)

где  жесткость при изгибе; С и D  константы интегрирования, которые представляют собой прогиб и угол поворота в начале координат и определяются из граничных условий задачи.

Вопросы для самопроверки

1. Как формулируется гипотеза плоских сечений?

2. Что представляют собой нейтральный слой и нейтральная линия и как они расположены?

3. По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они изменяются по высоте балки?

4. Что называется моментом сопротивления при изгибе и какова его размерность?

5. По какой формуле определяются нормальные напряжения в поперечных сечениях балки при поперечном изгибе?

6. Запишите формулу для определения касательных напряжений в поперечных сечениях балки при прямом поперечном изгибе?

7. Как находятся главные напряжения при изгибе?

1. Как направлены главные площадки на уровне нейтрального слоя и в точках, наиболее удаленных от этого слоя?

2. Какие формы поперечных сечений являются рациональными для балок из пластичных материалов?

3. Какие перемещения получают поперечные сечения балок при прямом изгибе?

4. Запишите основное дифференциальное уравнение изогнутой оси балки.

5. Что называется жесткостью сечения при изгибе?

6. Из каких условий определяются постоянные интегрирования, входящие в уравнение углов поворота и прогибов сечений балки?

Лекция 8 Плоский изгиб: построение эпюр поперечной силы и изгибающего момента

Построение эпюр поперечной силы и изгибающего момента; правила проверки эпюр

Как уже было сказано, при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора Q_y и M_x.

П

Рисунок 8.1

еред определением Q_y и M_x определяют реакции опор балки (рис. 8.1,а), составляя уравнения равновесия статики.

Для определения данных усилий используем два уравнения равновесия:

1. ; ;

.

2. ;

; .

Для определения Q_y и M_x применяют метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например, на расстоянии x от левой опоры. Отбросим одну из частей балки, например правую, и рассмотрим равновесие левой части (рис. 8.1, б). Взаимодействие частей балки заменим внутренними усилиями Q_y и M_x.

Таким образом,

а) поперечная сила Q_y в поперечном сечении балки численно равна алгебраической сумме проекций на поперечную ось сечения у всех внешних сил, действующих по одну сторону от сечения;

б) изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.

При практическом вычислении руководствуются обычно следующими правилами знаков для Q_y и M_x:

1. Если внешняя нагрузка стремится повернуть балку относительно рассматриваемого сечения по часовой стрелке, (рис. 8.2, б) то в выражении для Q_y она дает положительное слагаемое.

2. Если внешняя нагрузка создает относительно рассматриваемого сечения момент, вызывающий сжатие верхних волокон балки (рис. 8.2, а), то в выражении для M_z в этом сечении она дает положительное слагаемое.

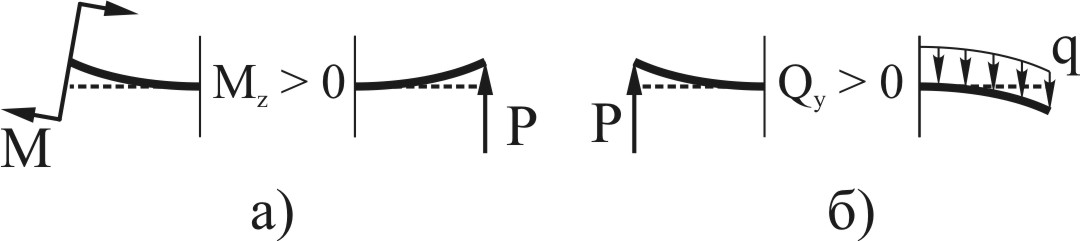
Рисунок 8.2