Лекция 7 Плоский изгиб: напряжения и прочность при изгибе

Напряжение при чистом изгибе; условие прочности при изгибе; напряжения при поперечном изгибе; полная проверка прочности балки; рациональные формы сечений балок; перемещения при плоском изгибе

Д

Рисунок 7.9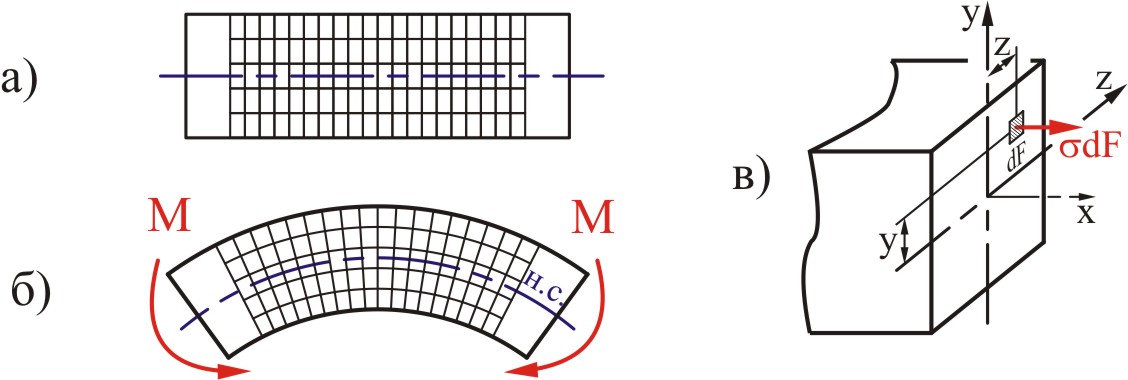

еформация изгиба заключается в искривлении оси прямого стержня или в изменении начальной кривизны прямого стержня (рис. 7.1).

Ознакомимся с основными понятиями, которые используются при рассмотрении деформации изгиба.

Стержни, работающие на изгиб, называют балками.

Чистым называется изгиб, при котором изгибающий момент является единственным внутренним силовым фактором, возникающем в поперечном сечении балки.

Чаще, в поперечном сечении стержня наряду с изгибающим моментом возникает также и поперечная сила. Такой изгиб называют поперечным.

Плоским (прямым) называют изгиб, когда плоскость действия изгибающего момента в поперечном сечении проходит через одну из главных центральных осей поперечного сечения.

При косом изгибе плоскость действия изгибающего момента пересекает поперечное сечение балки по линии, не совпадающей ни с одной из главных центральных осей поперечного сечения.

Изучение деформации изгиба начнем со случая чистого плоского изгиба.

7.1 Напряжение при чистом изгибе

Как уже было сказано, при чистом плоском изгибе в поперечном сечении из шести внутренних силовых факторов не равен нулю только изгибающий момент (рис. 7.1, в):

; (7.1)

Опыты, поставленные на эластичных моделях, показывают, что если на поверхность модели нанести сетку линий (рис. 7.1, а), то при чистом изгибе она деформируется следующим образом (рис. 7.1, б):

а) продольные линии искривляются по длине окружности;

б) контуры поперечных сечений остаются плоскими;

в) линии контуров сечений всюду пересекаются с продольными волокнами под прямым углом.

На основании этого можно предположить, что при чистом изгибе поперечные сечения балки остаются плоскими и поворачиваются так, что остаются нормальными к изогнутой оси балки (гипотеза плоских сечений при изгибе).

Определим нормальные напряжения, возникающие при чистом изгибе балки находящейся под действием моментов М_х.

В произвольной точке балки (рис. 7.2, т. А) в общем случае могут возникать нормальные напряжения как вдоль продольной оси σ_z, так и вдоль поперечных осей σ_x, σ_y. Однако экспериментально установлено, что нормальные напряжения σ_x, σ_y пренебрежимо малы по сравнению с напряжениями σ_z. Принимается так называемая гипотеза ненадавливания продольных волокон σ_x = 0, σ_y = 0. Поэтому можно принять, что материал балки находится при линейном напряженном состоянии вдоль оси z, и деформации подчиняются закону Гука. То есть нормальные напряжения при изгибе можно определить из формулы .

У становим закон изменения деформаций при изгибе балки.

При изгибе верхние волокна удлиняются, нижние укорачиваются, а продольная линия не меняет своей длины. Слой балки, не испытывающий при изгибе ни растяжения ни сжатия, называется нейтральным слоем. Линия пересечения нейтрального слоя и плоскости поперечного сечения называется нейтральной линией.

Определим относительную деформацию волокна ав ε_z (далее будем обозначать ее просто ε):

,

где r  радиус кривизны нейтрального слоя; у  расстояние от нейтрального слоя до рассматриваемого волокна балки.

Подставляя это соотношение в закон Гука, получим:

e

, (7.2)

т.е. напряжения s линейно зависят от координаты у.

Используя интегральную связь между напряжениями и изгибающим моментом:

,

подставляя в него соотношение (7.2), получим:

,

где  осевой момент инерции сечения.

Тогда получим выражение , подставляя которое в (7.2) окончательно имеем формулу для нормальных напряжений при изгибе:

.

Эпюра нормальных напряжений показана на рис. 7.2. Как видно, на нейтральной линии они равны нулю, максимального значения напряжения достигают в крайних верхних и нижних волокнах балки:

.

Обозначая , получим формулу для максимальных напряжений в произвольном сечении:

, (7.3)

где W_x – осевой момент сопротивления сечения изгибу, геометрическая характеристика поперечного сечения.