6.2 Условие прочности при кручении вала

При расчете на прочность при кручении необходимо знать максимальные напряжения для сравнения их с допускаемыми напряжениями. Очевидно, что максимальные напряжения при кручении круглого вала будут иметь точки максимально удаленные от оси вала. Т.е. точки с полярной координатой, равной радиусу сечения вала r:

.

Отношение полярного момента инерции J_ к наибольшему радиусу сечения r называется полярным моментом сопротивления W_:

. (6.12)

Тогда условие прочности при кручении будет иметь следующий вид:

. (6.13)

Для сплошного круглого сечения:

, (6.14)

. (6.15)

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором то при повороте граней элемента на 45 в новых площадках обнаруживаются только нормальные напряжения, равные по величине t (рис. 6.7).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис. 6.8,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45, т.е. по направлению действия максимальных растягивающих напряжений (рис. 6.8,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис. 6.8,в).

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным [] = [_р]  для хрупких материалов и [] = (0,50,6)[]  для пластичных материалов.

6.3 Деформации при кручении и условие жесткости

Если М_к = const и GJ_р = const по всей длине вала, то:

,

где GJ_р  жесткость вала при кручении.

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

.

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

. (6.16)

Эта формула выражает условие жесткости вала при кручении. Обычно принимается [] = 0,5 на 1 м длины вала.

6.4 Определение крутящего момента и построение эпюр крутящих моментов

Для определения напряжений и деформаций произвольного вала необходимо знать величину крутящих моментов на его отдельных участках.

Крутящий момент М_кр в произвольном сечении вала равен сумме внешних моментов М_к, расположенных по одну сторону сечения.

Крутящий момент М_кр считается положительным, если при наблюдении с торца вдоль оси рассматриваемой части он стремится вращать сечение по часовой стрелке (рис. 6.9).

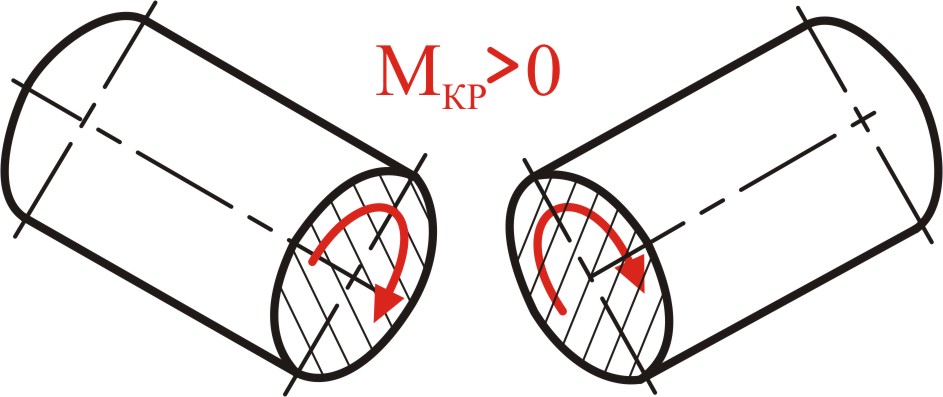
Рисунок 6.9

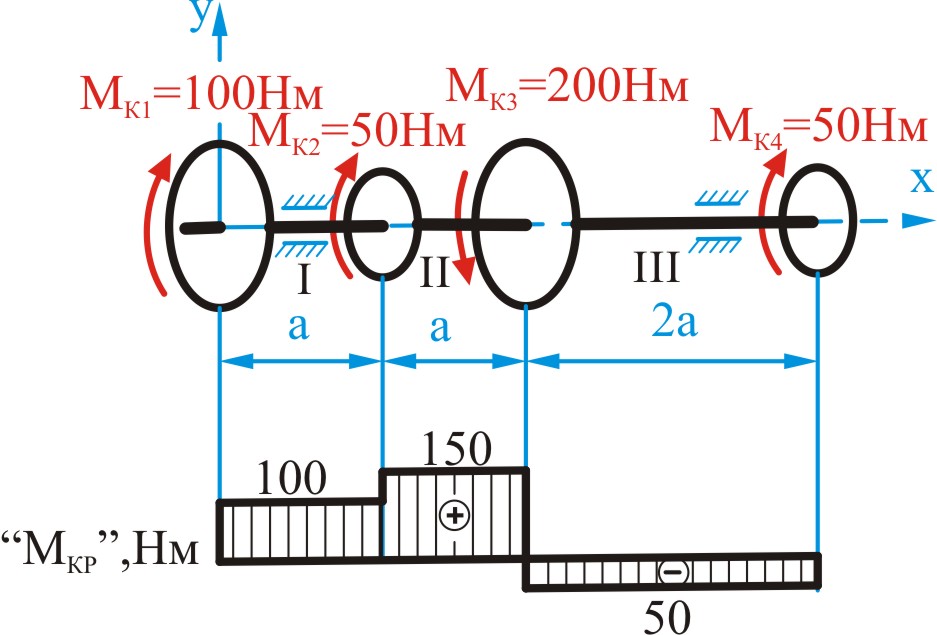
Рисунок 6.10

Рассмотрим в качестве примера построение эпюры крутящих моментов для трансмиссионного вала (рис. 6.10).

Разбиваем вал на участки , , .

Проведя произвольное сечение на первом участке:

, Н·м.

Для второго участка:

, Н·м.

На третьем участке рассматриваем правую часть от сечения, в котором определяем М_кр:

, Н·м.

Построенная эпюра показывает, что хотя к валу и приложен момент Н·м, наибольший крутящий момент в сечении равен лишь Н·м. Эту величину и следует использовать при расчете на прочность и жесткость.