5.8.3 Расчет сварного соединения

На срез принято рассчитывать и некоторые сварные соединения.

Если не учитывать наплывы, то в разрезе угловой шов имеет форму равнобедренного прямоугольного треугольника (рис. 5.9, а).

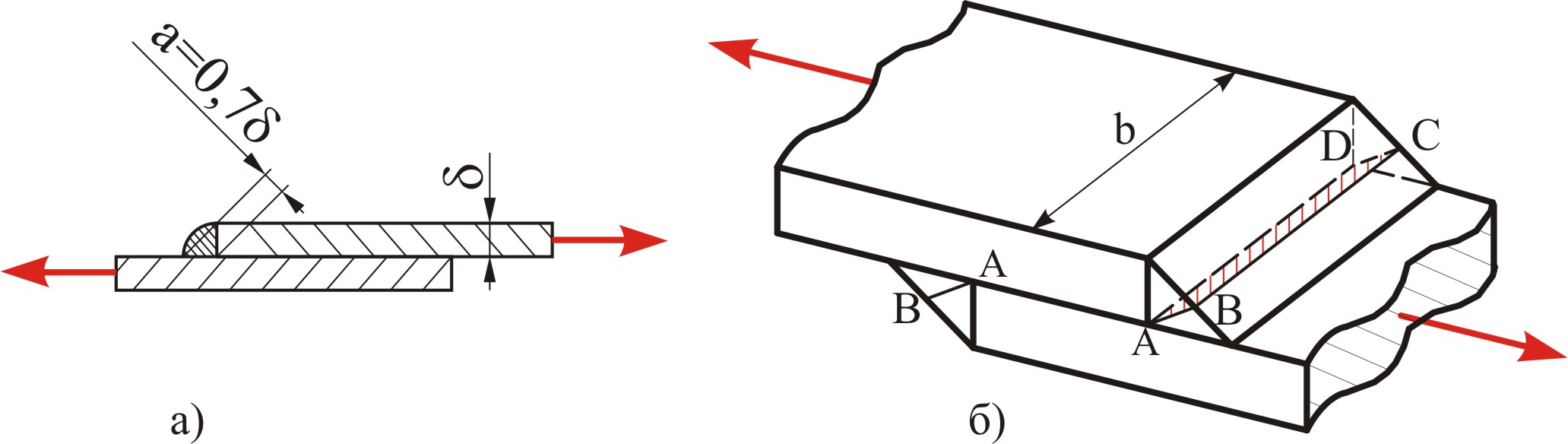
Рисунок 5.9

Разрушение шва будет происходить по его минимальному сечению ABCD (рис. 5.9, б), высота которого:

.

Для нахлесточного соединения в расчет вводят оба шва. Запишем условие прочности шва:

, (5.24)

где l_т  расчетная длина торцевого шва;  допускаемое напряжение для сварных соединений.

5.8.4 Конструирование болта

Обоснуем соотношение между диаметром d и высотой головки h болта (рис. 5.10), если [] = 0,6[].

С

Рисунок 5.10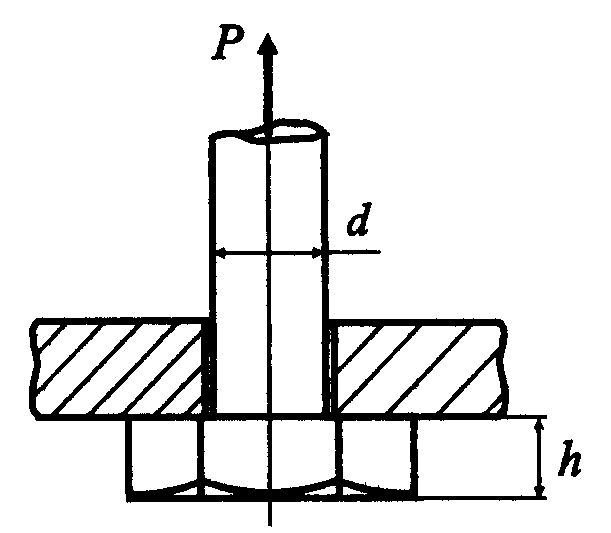

рез головки болта происходит по цилиндрической поверхности F_cp = dh. Условие прочности на срез имеет вид:

.

Условие прочности на растяжение стержня:

.

Предельное отношение касательных и нормальных напряжений определяет искомое соотношение между высотой головки болта и его диаметром (рис. 5.10):

; .

Вопросы для самопроверки

1. Что представляют собой теории прочности?

2. Сформулируйте первую и вторую теории прочности. Укажите область применения.

3. Сформулируйте третью и четвертую теории прочности? Укажите область применения этих теорий.

4. Какие силовые факторы могут вызвать деформацию сдвига.

5. Какие напряжения возникают при сдвиге.

6. Как производят расчеты на прочность при сдвиге.

7. Получите основные соотношения между диаметром болта и высотой его головки исходя из обеспечения прочности.

Лекция 6 Кручение

Напряжения в поперечном сечении; условие прочности; деформации условие жесткости; определение крутящего момента и построение эпюр крутящих моментов; расчет винтовых цилиндрических пружин с небольшим шагом

Д еформация кручения вызывается парами сил, плоскости действия которых перпендикулярны к оси стержня. Поэтому при кручении в произвольном поперечном сечении стержня из шести внутренних силовых факторов возникает только один – крутящий момент M_к (рис. 6.1). Как показывают опыты, поперечные сечения при кручении поворачиваются одно относительно другого вокруг оси стержня, при этом длина не меняется.

Стержни, работающие на кручение, обычно называют валами.

Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. В большинстве случаев бывают заданы мощность, передаваемая валом, и числом оборотов, а величины скручивающих моментов определяются исходя из этих данных.

Пусть вал вращается с постоянной скоростью n (об/мин) и передает мощность N (Нм/с). Угловая скорость вращения вала равна (рад/сек), а передаваемая мощность . Скручивающий момент равен .

6.1 Напряжения в поперечном сечении

Р

Рисунок 6.2

Рисунок 6.3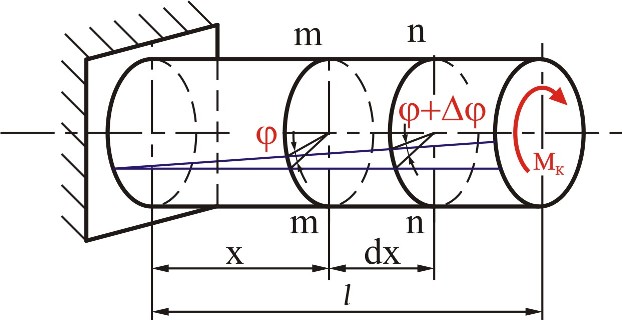

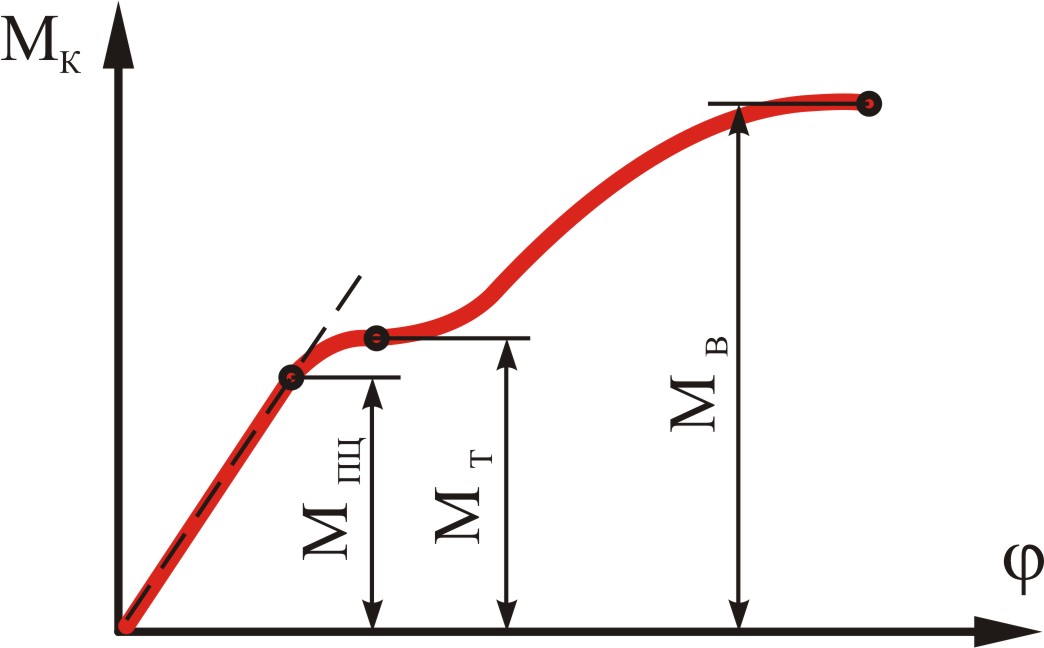
ассматривая кручение вала, легко установить, что под действием скручивающего момента любое сечение на расстоянии х от заделки поворачивается относительно закрепленного сечения на некоторый угол   угол закручивания (рис. 6.2). При этом чем больше скручивающий момент M_к, тем больше и угол закручивания. Зависимости , называемые диаграммами кручения, полученные для образца из пластичного материала, до некоторой степени подобны диаграммам растяжения (рис. 6.3). В дальнейшем при выводе формул для напряжений и угла закручивания нас будет интересовать участок диаграммы кручения, соответствующий работе материала в пределах пропорциональности.

Рассмотрим геометрическую картину деформации вала при кручении.

Е

Рисунок 6.4

сли до деформации на поверхность вала нанести сетку, состоящую из линий, параллельных оси, и линий, представляющие собой параллельные круги, то после закручивания вала скручивающим моментом M_к можно заметить следующее: образующие цилиндра превращаются в винтовые линии, параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях остаются прямыми (рис. 6.4).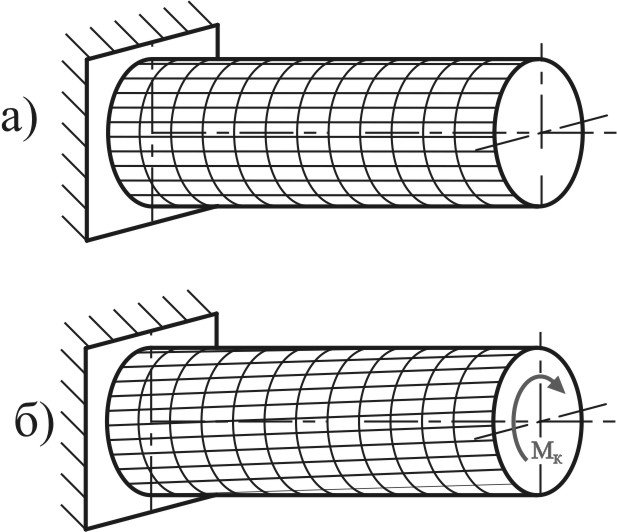

Полагая, что картина, наблюдаемая на поверхности вала, сохраняется и внутри, сформулируем гипотезы, взятые в основу теории кручения круглых стержней:

1. Поперечные сечения, плоские и нормальные к оси вала до деформации, остаются плоскими и нормальными к той же оси и после деформации.

2. Прямолинейная ось вала остается прямолинейной и после деформации, а все поперечные сечения поворачиваются вокруг этой оси по отношению друг к другу на какой то угол d.

3. Радиусы поперечных сечений при деформации не искривляются.

4. Расстояния между сечениями вала в процессе деформации не изменяются, следовательно, и вся длина вала остается прежней.

Н

Рисунок 6.5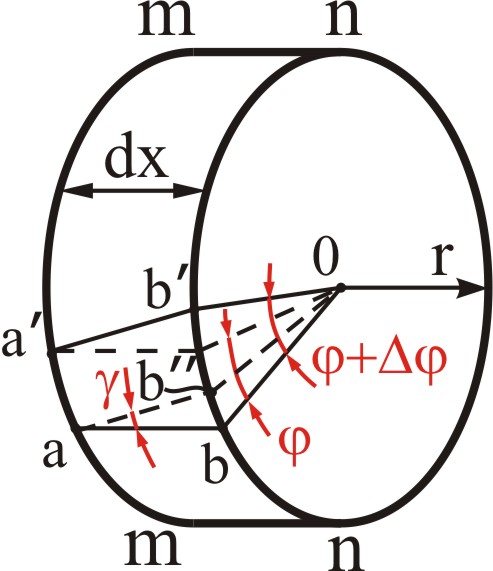

а основании принятых гипотез кручение круглого вала можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения, а нормальные напряжения равны нулю.

Выделим из закручиваемого вала диск радиуса r на расстоянии x от закрепленного конца, ограниченный двумя смежными сечениями m-m и n-n, находящимися друг от друга на расстоянии dx (рис. 6.5) и рассмотрим его отдельно.

Если сечение m-m, лежащее на расстоянии x от защемленного конца вала, повернулось относительно последнего на угол , то сечение n-n, находящееся на расстоянии , повернется относительно закрепленного конца на угол .

Точки и до деформации лежащие на одной образующей, после деформации расположатся на винтовой линии и займут новое положение a и b.

Проведем от точки a прямую ab, параллельную ab и соединим центр сечения n-n с точкой b. Тогда угол bOb, равный d, будет углом поворота сечения n-n относительно сечения m-m. У элемента abba до поворота сечения n-n относительно сечения m-m верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение ab и ab. Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:

.

Относительный сдвиг будет равен:

.

Отношение представляет относительный угол закручивания  (угол закручивания на единицу длины бруса). Тогда

. (6.1)

Из этой формулы видно, что относительный сдвиг пропорционален радиусу закручиваемого цилиндрического тела.

На основании закона Гука для сдвига:

. (6.2)

Можно определить касательное напряжение для элементов лежащих на поверхности вала:

Рисунок 6.6

. (6.3)

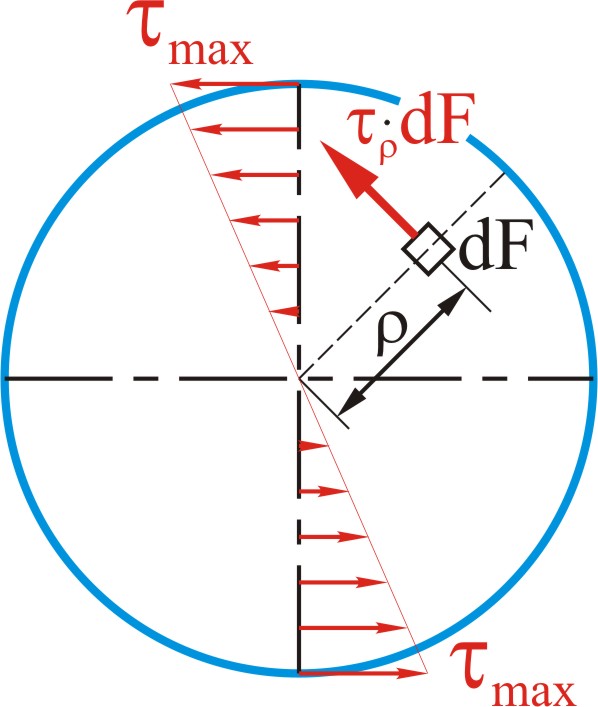
Учитывая предположение, что деформация элементов на поверхности вала подобна деформации элементов внутри вала, для произвольного элемента, находящегося на расстоянии  от центра поперечного сечения (рис 6.6):

, (6.4)

. (6.5)

Касательная элементарная сила на площадке dF расположенной на расстоянии  от оси вала:

.

Момент элементарной силы относительно оси бруса будет:

. (6.6)

Сумма таких элементарных моментов, распределенных по всему поперечному сечению F, при равновесии, наступающем после деформации, должна быть равна крутящему моменту:

. (6.7)

Вынесем постоянные за знак интеграла, получим:

. (6.8)

Интеграл является полярным моментом инерции J_. Тогда

. (6.9)

Откуда относительный угол закручивания:

. (6.10)

Подставляя в выражение (6.5) выражение относительного угла закручивания получим

. (6.11)

Это уравнение показывает, что напряжения в площадках сечения прямо пропорциональны их расстояниям до центра сечения.

Анализируя эпюру касательных напряжений (рис. 6.6) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.