5.6 Анализ напряженного состояния при сдвиге

Рисунок 5.5  Напряженное

состояние чистого сдвига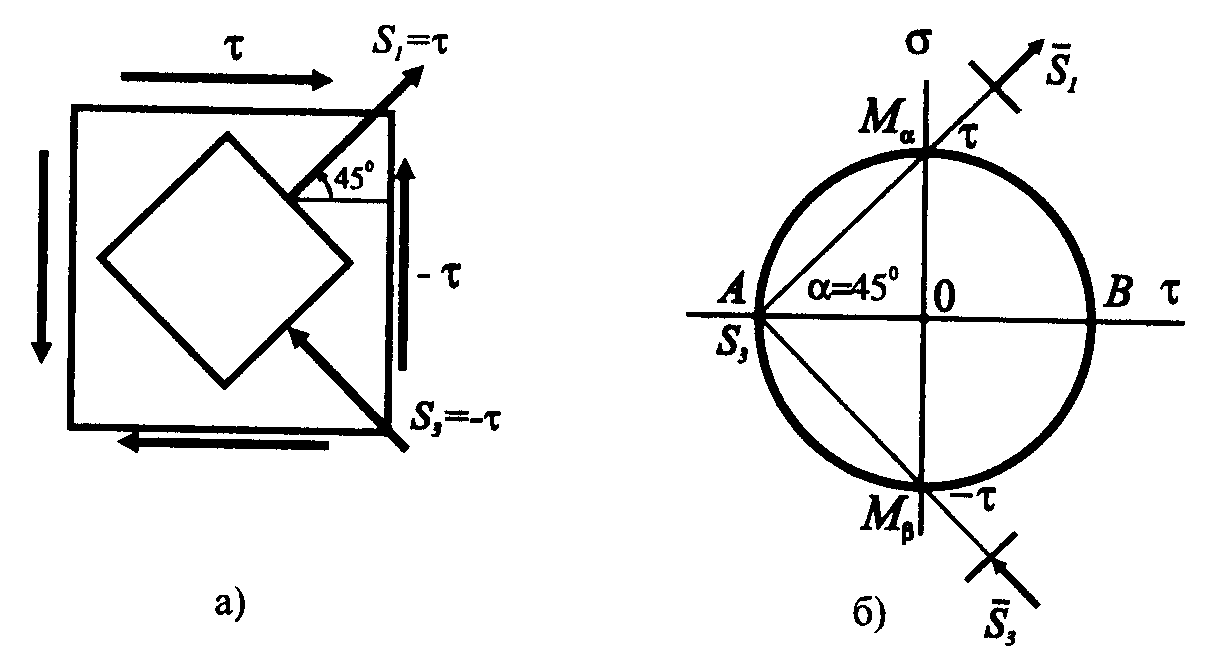

Если по граням элемента действуют только касательные напряжения (рис. 5.5), то такой вид напряженного состояния называется чистым сдвигом. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига.

Анализ показывает, что при чистом сдвиге возникает плоское напряженное состояние. Главные площадки наклонены под углом 45° к направлению площадок чистого сдвига (tg2₀ = ).

5 Рисунок 5.6  Соединение двух листов заклепками .7 Расчет на прочность

при сдвиге

Условие прочности при сдвиге имеет вид:

, (5.13)

где []  допускаемое касательное напряжение, которое в первом приближении принимается равным [] = (0,5…0,6)[].

5.8 Примеры расчета

5.8.1 Расчет заклепочного соединения

На рис. 5.6 показано соединение двух листов заклепками (соединение внахлест), которое разрушается в результате перерезывания заклепок по линии соприкосновения листов. Если разрушение каждой заклепки происходит по одной плоскости среза, то заклепочное соединение называется односрезным, если по двум плоскостям, то соединение называется двухсрезным и т.д.

Для упрощения задачи принимаем, что по плоскостям среза действуют только касательные напряжения, которые распределяются по поверхности среза равномерно, а также что при действии статической нагрузки можно принять поперечную силу в каждой заклепке равной:

, (5.14)

где Р  сила, действующая на соединение; п  число заклепок.

Условие прочности заклепок на срез:

, (5.15)

где F =  d ²/4  площадь поперечного сечения заклепки диаметром d; [] = (0,60,8)[]  допускаемое касательное напряжение.

При двухсрезном или многосрезном заклепочном соединении вместо п в формулу (5.15) следует подставлять общее число срезов заклепок, расположенных по одну сторону стыка.

З

Рисунок 5.7  Распределение

напряжений смятия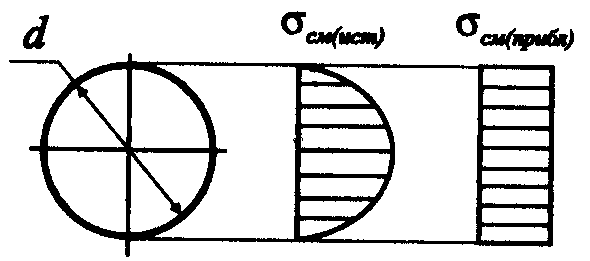

аклепочные соединения рассчитывают также на смятие. Проверяют напряжения смятия по площади соприкосновения соединяемых листов и заклепок. Для приближенного расчета истинная эпюра распределения сжимающих напряжений смятия заменяется приближенной равномерной эпюрой (рис. 5.7). Площадь смятия одной заклепки принимают равной:

,

где t  толщина соединяемых листов.

Условие прочности на смятие имеет вид:

, (5.16)

где [_см]  допускаемое напряжение на смятие, [_см] = (22,5)[].

В случае склепывания внахлест двух листов различной толщины принимают t = t_min.

Условие прочности листа на разрыв:

, (5.17)

где F₁  площадь сечения листа по ряду заклепок в направлении, перпендикулярном линии действия силы Р; п₁  число заклепок в этом сечении; b  ширина листа (см. рис. 5.6).

5.8.2 Расчет болтового соединения

В качестве примера рассмотрим расчет болтового соединения, приведенного на рис. 5.8.

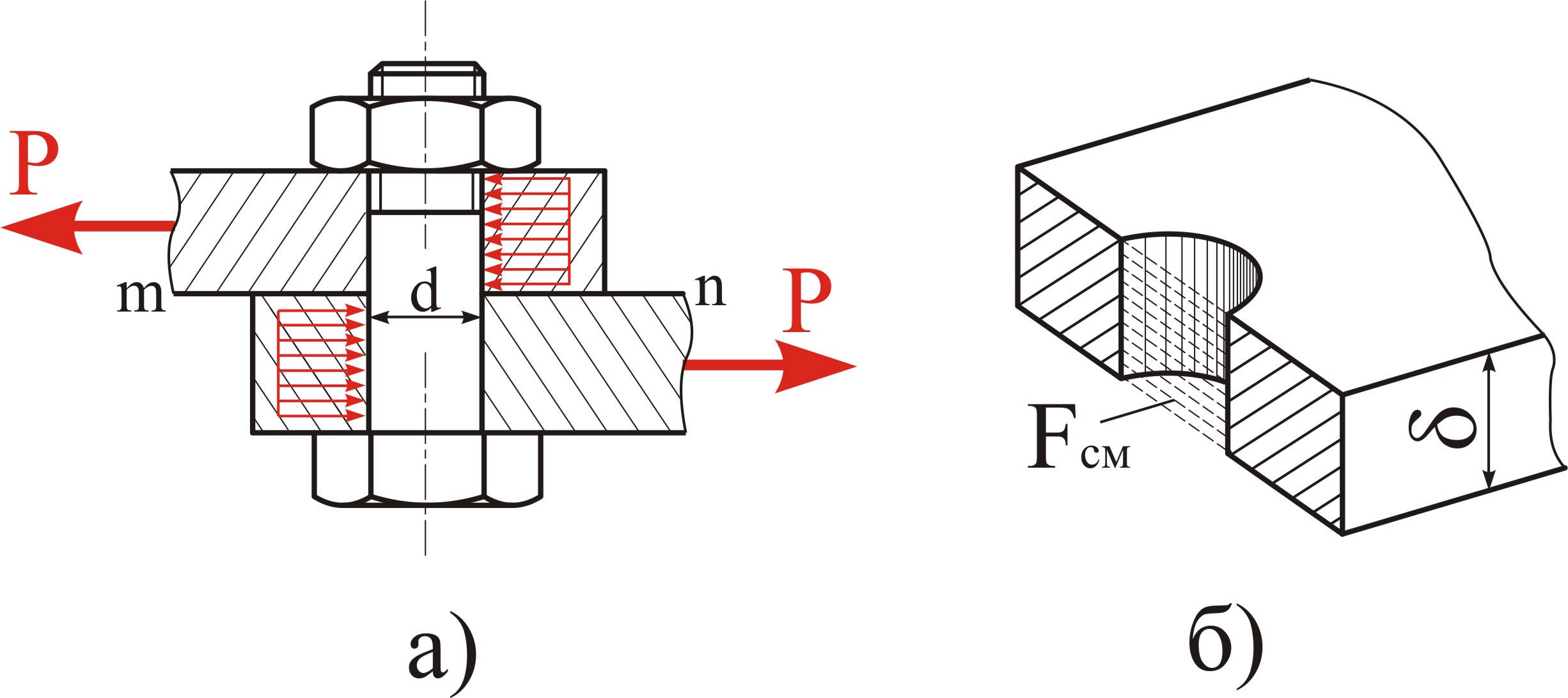
Рисунок 5.8

Силы Р стремятся сдвинуть листы относительно друг друга. Этому препятствует болт, на который со стороны каждого листа передаются распределенные по контактной поверхности силы, равнодействующие которых равны Р. Усилия стремятся срезать болт в плоскости раздела листов m  n, так как в этом сечении действует максимальная поперечная сила Q = Р. Считая, что касательные напряжения распределены равномерно, получим:

. (5.18)

Таким образом, условие прочности болта на срез принимает вид:

. (5.19)

Отсюда можно найти диаметр болта:

. (5.20)

При расчете болтовых соединений следует учитывать, что нагрузки, приложенные к элементам соединений, помимо среза вызывают смятие контактирующих поверхностей. Под смятием понимают пластическую деформацию, возникающую на поверхностях контакта.

Максимальное напряжение смятия на цилиндрических поверхностях:

,

где F_см  площадь проекции поверхности контакта на диаметральную плоскость (рис. 5.8,б):

. (5.21)

Условие прочности на смятие имеет вид:

. (5.22)

Допускаемые напряжения на смятие устанавливают опытным путем и принимают равным .

На основании зависимости (5.22) получим:

. (5.23)

Чтобы были удовлетворены условия прочности на срез и на смятие, из двух найденных диаметров следует взять больший, округлив его до стандартного значения.