5.4 Четвертая гипотеза прочности: гипотеза потенциальной энергии

формоизменения

Причиной наступления предельного напряженного состояния материала является достижение удельной потенциальной энергией формоизменения своей критической величины.

Гипотеза основывается на предположении о том, что количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состояния в материале, одинаково как при любом сложном напряженном состоянии, так и при простом растяжении.

Гипотеза связывается с развитием только пластических деформаций, характеризующихся изменением формы тела без изменения объёма.

Полная удельная потенциальная энергия состоит из двух частей:

, (5.5)

где  энергия, вызывающая только изменения объема;  энергия, вызывающая только изменения формы кубика с ребром равным единице.

Условие отсутствия пластических деформаций:

,

где U_Ф  расчетная величина энергии формоизменения для исследуемого напряженного состояния; U_ФО  предельное опытное значение той же энергии при одноосном растяжении.

В общем случае напряженного состояния энергия формоизменения определяется по формуле:

.

В случае предельного состояния текучести при простом растяжении:

,

где ₀ – предельное опытное значение напряжения при одноосном растяжении.

Условие прочности:

, (5.6)

где [] – допускаемое напряжение при растяжении.

В частном случае плоского напряженного состояния при _у = 0, _х = , _ху =  условие прочности записывается в виде:

. (5.7)

Гипотеза удельной потенциальной энергии формоизменения хорошо согласуется с опытом для пластических материалов и широко используется в настоящее время.

5.5 Определение внутренних сил, напряжений и деформаций при сдвиге

С

Рисунок 5.2  Сдвиг (срез)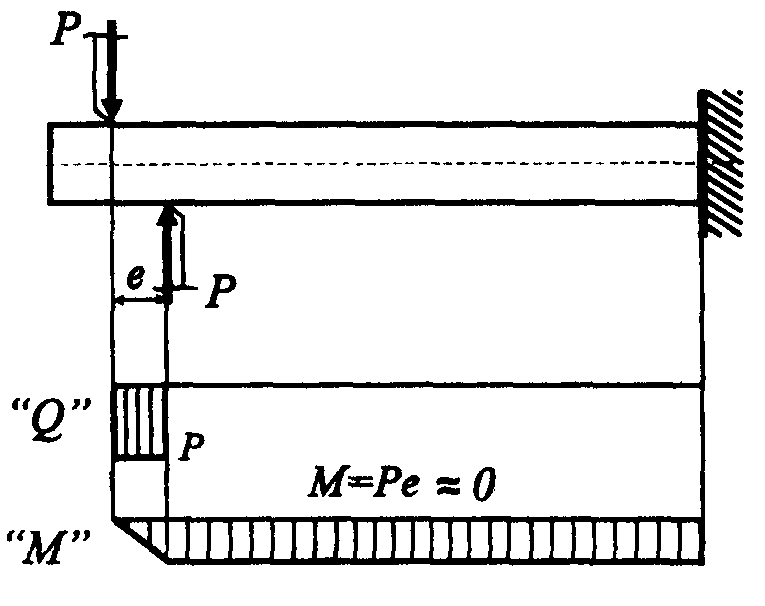

двигом называется такой вид нагружения бруса, при котором в его поперечных сечениях из шести составляющих главного вектора и главного момента внутренних сил, от нуля отличается только поперечная сила. Данный вид нагружения встречается редко и чаще всего он сопровождается изгибающими моментами. Однако, в некоторых случаях, например, в заклепочных и сварных соединениях при раскройных работах имеет место близкое к сдвигу нагружение бруса (рис. 5.2).

В

Рисунок 5.3  Распределение касательных напряжений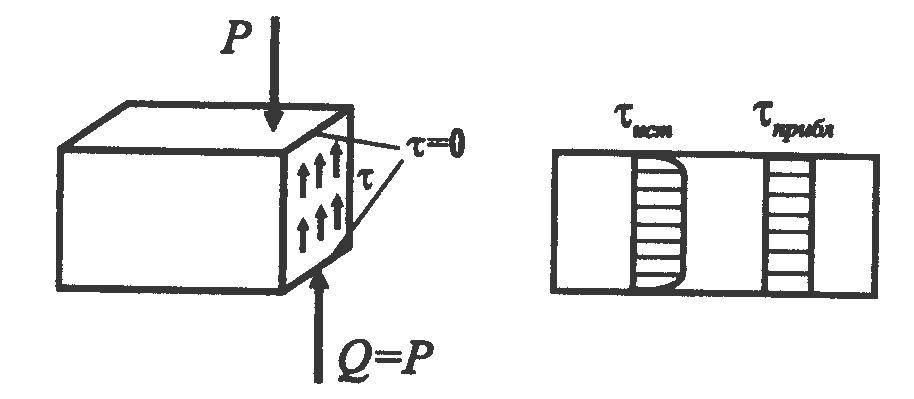

нутренняя поперечная сила Q в поперечном сечении бруса на участке действия сосредоточенных сил определяется методом сечений и равна Р. Если расстояние между сосредоточенными силами (например, расстояние между ножами при раскрое материала) мало, то можно пренебречь величиной изгибающего момента. При этом распределение касательных напряжений по сечению неравномерно, так как внешняя поверхность бруса свободна от осевой нагрузки и по закону парности касательных напряжений, в верхних и нижних точках сечения касательные напряжения равны нулю (рис. 5.3).

Как показывают исследования, распределение касательных напряжений весьма близко к равномерному закону (рис. 5.3) и поэтому в первом приближении для упрощения расчетов заменяется равномерным законом распределения. Тогда

.

Таким образом, касательное напряжение при сдвиге (срезе) определяется уравнением:

, (5.8)

где F  площадь среза.

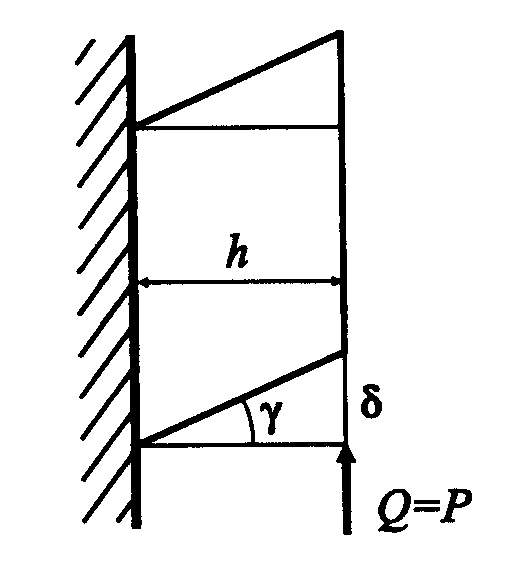
Деформация бруса при сдвиге в зоне действия усилия, предшествующая разрушению от среза, заключается в перекашивании прямых углов элемента (рис. 5.4).

Аналогично растяжению (сжатию) закон Гука при сдвиге в абсолютных координатах имеет вид:

Рисунок 5.4  Деформация бруса

при сдвиге:   абсолютный сдвиг;

tg =    / h  относительный

сдвиг или угол сдвига

. (5.9)

где G  модуль сдвига или модуль упругости второго рода.

Модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, что подтверждают опыты, уравнением:

. (5.10)

Для стали модуль сдвига примерно равен 810⁴ МПа. Из уравнения (5.9) с учетом (5.8) может быть получен закон Гука при сдвиге в относительных координатах:

, (5.11)

или

. (5.12)

Закон Гука справедлив лишь до предела пропорциональности. При испытаниях на сдвиг образцов из пластичных материалов так же, как и при растяжении, имеет место явление текучести. Предел текучести обозначается _т, а предел прочности  _в.