3.7 Понятие о радиусе инерции
Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции:
(3.24)
где
радиус инерции
относительно оси х.
Из выражения (3.24) следует, что
. (3.25)
Аналогично радиус инерции площади
сечения относительно оси
:
. (3.26)
Главным центральным осям инерции соответствуют главные радиусы инерции:
,
. (3.27)
3.8 Моменты сопротивления площади
Осевым моментом сопротивления площади сечения F относительно главной центральной оси называется отношение момента инерции площади относительно этой же оси к расстоянию до наиболее удаленной точки от этой оси:
. (3.28)
Момент сопротивления измеряется в м3.
Отношение полярного момента инерции площади сечения к наибольшему радиусу вектору этой площади, называется полярным моментом сопротивления:
. (3.29)
Для площади прямоугольника:
, 
.
Для площади круга:
, 
, 
.
3.9 Моменты инерции сечений сложной формы
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:
, (3.30)
что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры необходимо разбить её на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.
Пусть требуется определить моменты инерции сложной фигуры относительно осей X, Y (рис. 3.11). При вычислении моментов инерции сложных сечений их нужно разбить на простые части, моменты инерции которых известны.
И
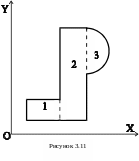з
основного свойства интеграла суммы
следует, что момент инерции сложной
фигуры равен сумме моментов инерции
составных ее частей:
;
.
Если в сечении имеется отверстие (рис. 3.12), то его удобно считать фигурой с отрицательной площадью:
;
.
3 .10 Стандартные прокатные профили
Нашей промышленностью выпускаются стандартные прокатные профили (рис. 3.13) (двутавр, швеллер, уголок равнобокий, уголок неравнобокий), которые могут быть использованы как готовые элементы конструкций (балки, стойки, элементы ферм и т.д.). Размеры прокатных профилей стандартизированы и сведены в таблицы сортаментов прокатной стали, которые приводятся в приложениях почти всех учебников и сборников задач по сопротивлению материалов. В этих таблицах приводятся все размеры сечений и основные геометрические характеристики прокатных профилей в соответствии с их номером.
|
|
|
|
двутавр |
швеллер |
Равнобокий уголок |
неравнобокий уголок |
Рисунок 3.13
Вопросы для самопроверки
Геометрические характеристики плоских сечений.
Центробежные моменты, моменты инерции, моменты сопротивления.
Статические моменты сечений.
Зависимость между моментами инерции относительно параллельных осей.
Изменение моментов инерции сечения при повороте осей координат.
Главные оси инерции и главные моменты инерции.
Моменты инерции простых сечений.
Лекция 4 Основы теории напряженного состояния
Напряжения в точке, тензор напряжений; закон парности касательных напряжений, главные площадки и главные напряжения; линейное, плоское и объемное напряженные состояния; обобщенный закон Гука
4.1 Напряжения в точке. Тензор напряжений
Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечного малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. 4.1.
С
Рисунок
4.7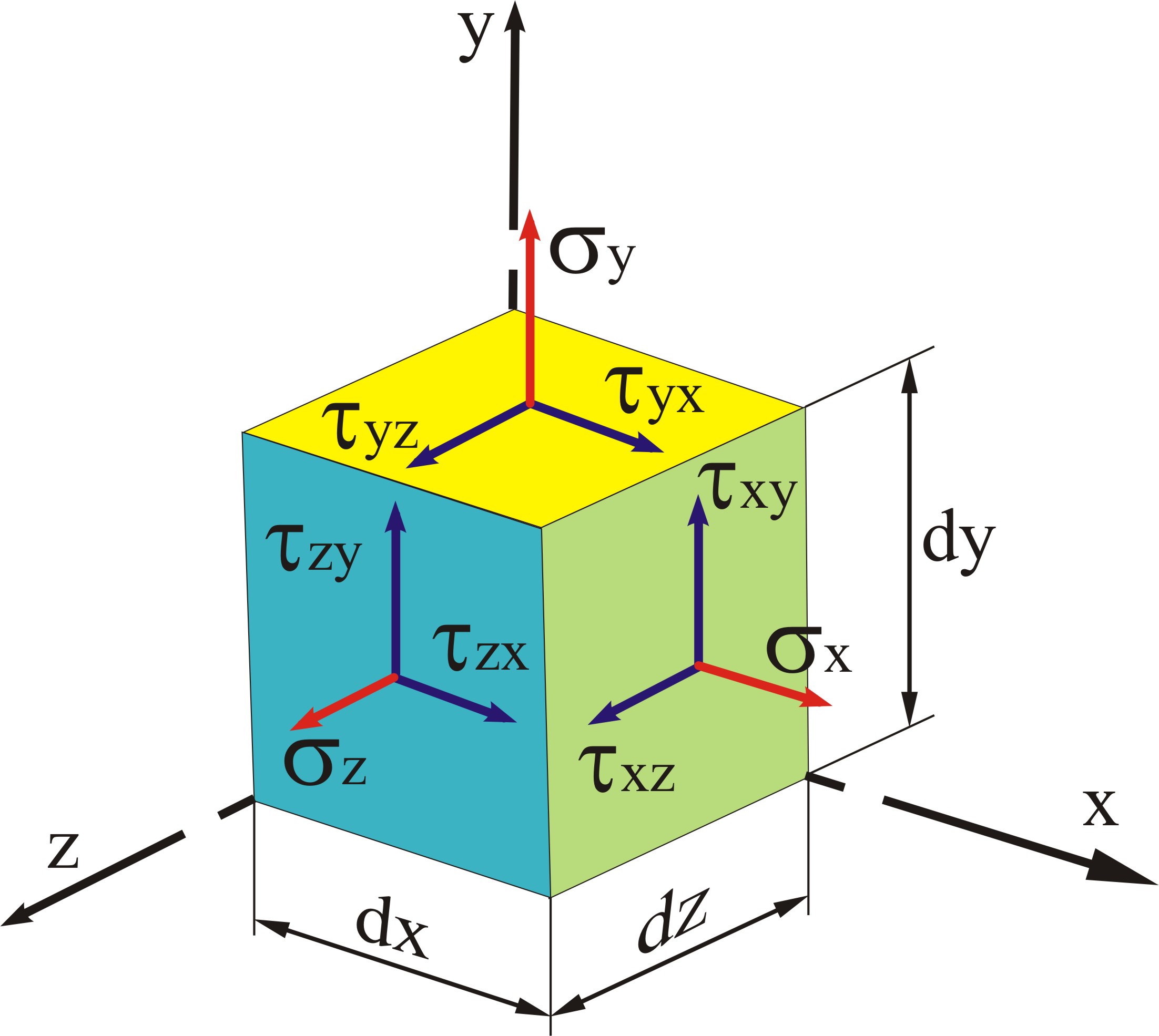
Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действуют девять компонентов напряжения. Запишем их в виде следующей квадратной матрицы:
,
где в первой, второй и третьей строках расположены составляющие напряжений соответственно на площадках, перпендикулярных к осям х, у, z. Эта совокупность напряжений называется тензором напряжений.
Нормальное напряжение считается положительным, если оно направлено от площадки. Касательное напряжение считается положительными, если изображающий его вектор стремится вращать параллелепипед по часовой стрелки относительно любой точке, лежащей внутри параллелепипеда. Отрицательными считаются напряжения обратных направлений.