3 .4.3 Круг

Определим сначала полярный момент инерции относительно центра круга (рис. 3.8). За dF примем площадь бесконечно тонкого кольца толщиной dr, расположенного на расстоянии r от центра круга .

Тогда

. (3.15)

Теперь определим осевые моменты инерции. Очевидно, что в силу симметрии ; но . Откуда

. (3.16)

3.4.4 Кольцо

Определим моменты инерции кольца, у которого R  наружный радиус, r  внутренний радиус (рис. 3.9). Интегрируя полученное ранее выражение для полярного момента инерции в пределах от r до R, получим:

.

Это выражение может быть представлено в виде:

, (3.17)

где .

Соответственно

. (3.18)

3.5 Изменение моментов инерции при

Рисунок 3.10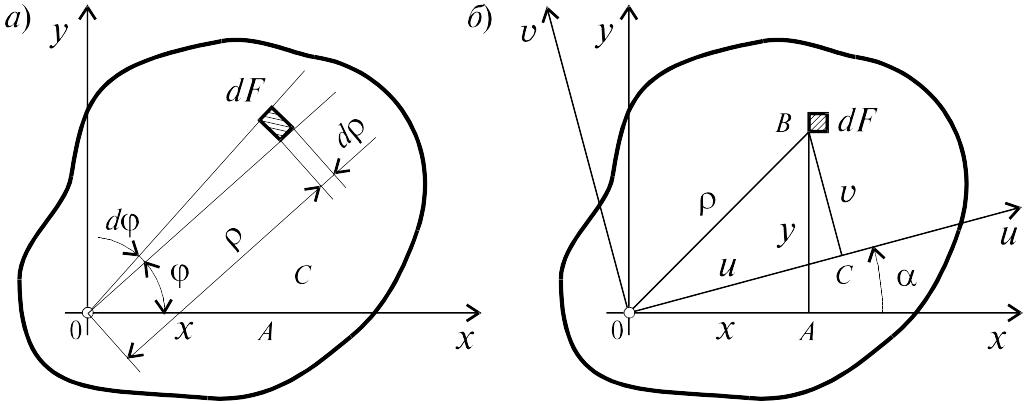

повороте осей координат

Пусть задана система координат и известны моменты инерции J_х, J_у и J_хy фигуры относительно осей координат. Повернем оси координат на некоторый угол  против часовой стрелки и определим моменты инерции той же фигуры относительно новых осей и и v (рис. 3.10).

Координаты точки в этих системах координат связаны уравнениями:

.

Момент инерции:

,

или

, (3.19)

и

, (3.20)

Центробежный момент инерции:

, (3.21)

Из полученных уравнений видно, что , т.е. сумма осевых моментов инерции при повороте осей координат остается величиной постоянной. Поэтому, если относительно какой-либо оси момент инерции достигает максимума, то относительно перпендикулярной ей оси он имеет минимальное значение.

3.6 Главные оси и главные моменты инерции

Из формул (3.19), (3.20), (3.21) видно, что при повороте осей координат центробежный момент инерции меняет знак, а, следовательно, существует такое положение осей, при котором центробежный момент равен нулю.

Оси, относительно которых центробежный момент инерции сечения обращается в нуль, называются главными осями, а главные оси, проходящие через центр тяжести сечения  главными центральными осями инерции сечения.

Моменты инерции относительно главных осей инерции сечения называются главными моментами инерции сечения и обозначаются J₁ и J₂ причем J₁ > J₂.

Предположим, что оси и и v главные. Тогда

,

, (3.22)

Уравнение (3.22) определяет положение главных осей инерции сечения в данной точке относительно исходных осей координат. При повороте осей координат изменяются также и осевые момента инерции. Найдем положение осей, относительно которых осевые моменты инерции достигают экстремальных значений. Для этого возьмем первую производную от J_u по  и приравняем ее нулю:

,

тогда

.

К тому же результату приводит и условие . Сравнивая последнее выражение с формулой (3.22), можно сделать вывод, что главные оси инерции являются осями, относительно которых осевые моменты инерции сечения достигают экстремальных значений.

Исключая из формул (3.19), (3.20), (3.21) тригонометрические функции, получим:

. (3.23)

Знак плюс в формуле (3.23) соответствует большему (J₁), а знак минус  меньшему (J₂) моментам инерции сечения.

Нетрудно доказать, что если моменты инерции сечения относительно главных осей одинаковы, то все оси, проходящие через ту же точку сечения, являются главными и осевые моменты инерции относительно всех этих осей одинаковы: J_u = J_v = J_y = J_х. Этим свойством обладают квадратные, круглые и кольцевые сечения.