
- •Лекция 1 Задачи сопротивления материалов. Растяжение и сжатие
- •1.1 Основные формы элементов конструкций
- •1.2 Основные виды деформаций
- •1.3 Основные гипотезы науки о сопротивлении материалов
- •1.4 Классификация внешних сил
- •1.5 Опоры и реакции
- •1.6 Внутренние силы. Метод сечений
- •1.7 Напряжение
- •1.8 Растяжение и сжатие
- •1.9 Нормальные напряжения. Условие прочности
- •1.10 Основные типы расчетов на прочность
- •Вопросы для самопроверки
- •Лекция 2 Опытное изучение механических свойств материалов
- •2.1 Опытное изучение свойств материалов при одноосном растяжении
- •2.2 Диаграмма растяжения стали марки Ст3
- •2.3 Наклеп
- •2.4 Диаграммы растяжения других конструкционных материалов
- •2.5 Испытание конструкционных материалов на сжатие
- •2.6 Определение твердости
- •Твердости по Виккерсу
- •2.7 Деформации при растяжении (сжатии)
- •Вопросы для самопроверки
- •Лекция 3 Геометрические характеристики плоских сечений
- •3.1 Статические моменты сечений
- •3.2 Моменты инерции сечений
- •3.3 Зависимость между моментами инерции относительно параллельных осей
- •3.4 Моменты инерции простых сечений
- •3.4.1 Прямоугольник
- •3.4.2 Треугольник
- •3 .4.3 Круг
- •3.4.4 Кольцо
- •3.5 Изменение моментов инерции при
- •3.6 Главные оси и главные моменты инерции
- •3.7 Понятие о радиусе инерции
- •3.8 Моменты сопротивления площади
- •3.9 Моменты инерции сечений сложной формы
- •3 .10 Стандартные прокатные профили
- •4.2 Закон парности касательных напряжений. Главные площадки и главные напряжения
- •4.3 Линейное напряженное состояние Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис. 4.2, в).
- •4.4 Плоское напряженное состояние
- •4.5 Объемное напряженное состояние
- •5.1 Первая гипотеза прочности: гипотеза наибольших нормальных
- •5.2 Вторая гипотеза прочности: гипотеза наибольших удлинений
- •5.3 Третья гипотеза прочности: гипотеза наибольших касательных
- •5.4 Четвертая гипотеза прочности: гипотеза потенциальной энергии
- •5.5 Определение внутренних сил, напряжений и деформаций при сдвиге
- •5.6 Анализ напряженного состояния при сдвиге
- •5 Рисунок 5.6 Соединение двух листов заклепками .7 Расчет на прочность
- •5.8 Примеры расчета
- •5.8.1 Расчет заклепочного соединения
- •5.8.2 Расчет болтового соединения
- •5.8.3 Расчет сварного соединения
- •5.8.4 Конструирование болта
- •Вопросы для самопроверки
- •Лекция 6 Кручение
- •6.1 Напряжения в поперечном сечении
- •6.2 Условие прочности при кручении вала
- •6.3 Деформации при кручении и условие жесткости
- •6.4 Определение крутящего момента и построение эпюр крутящих моментов
- •6.5 Расчет винтовых цилиндрических пружин с небольшим шагом
- •Вопросы для самопроверки
- •Лекция 7 Плоский изгиб: напряжения и прочность при изгибе
- •7.1 Напряжение при чистом изгибе
- •7.2 Условие прочности при изгибе
- •7.3 Напряжения при поперечном изгибе
- •7.4 Полная проверка прочности балки
- •7.5 Рациональные формы сечений балок
- •7.6. Перемещения при плоском изгибе
- •Вопросы для самопроверки
- •Лекция 8 Плоский изгиб: построение эпюр поперечной силы и изгибающего момента
- •8.1. Построение эпюр поперечной силы и изгибающего момента
- •8.2 Правила проверки эпюр
- •Вопросы для самопроверки
- •Лекция 9 Сложное сопротивление
- •9.1 Сложный и косой изгиб
- •9.2 Внецентренное растяжение (сжатие) прямого бруса
- •9.3 Изгиб с кручением
- •Вопросы для самопроверки
- •Лекция 10 Устойчивость сжатых стержней: Продольный изгиб
- •10.1 Устойчивое и неустойчивое упругое равновесие
- •10.2 Формула Эйлера
- •10.3 Влияние способов закрепления концов стержня на критическую силу
- •10.4 Пределы применимости формулы Эйлера
- •10.5 Расчеты на устойчивость при помощи коэффициентов уменьшения основного допускаемого напряжения
- •10.6 Рациональные формы сечений стержней
- •Вопросы для самопроверки
- •Лекция 11 Динамическое нагружение
- •11.1 Понятие о динамическом действии нагрузки
- •11.2 Удар
- •11.3 Механические свойства материалов при ударе
- •11.4 Напряжения, изменяющиеся во времени. Явление усталости материалов
- •11.5 Влияние конструктивно-технологических факторов на предел усталости
- •11.5.1 Влияние концентрации напряжений
- •11.5.2 Влияние размеров (масштабный фактор)
- •11.5.3 Влияние состояния поверхности
- •11.5.4 Влияние пауз
- •11.5.5 Влияние температуры
- •11.6 Практические меры повышения сопротивления усталости
- •Вопросы для самопроверки
- •Лекция 12 Расчет на прочность при колебаниях
- •12.1 Основные понятия
- •12.2 Жесткость системы (коэффициент упругого сопротивления)
- •12.3 Жесткость системы при параллельном соединении упругих
- •12.4 Жесткость системы при последовательном соединении упругих
- •12.5 Свободные колебания систем с одной степенью свободы.
- •12.6 Логарифмический декремент затухания
- •12.7 Коэффициент динамичности
- •12.8 Виброактивность и виброзащита
- •Вопросы для самопроверки
3.2 Моменты инерции сечений
Моментами инерции сечения называются геометрические характеристики, определяемые интегралами вида:
![]() (3.6)
(3.6)
где Jx, Jy осевые (экваториальные) моменты инерции относительно осей х и у соответственно;
![]() ,
(3.7)
,
(3.7)
где Jр полярный момент инерции сечения относительно данной точки (полюса); r - расстояние от площадки dF до полюса (рис. 3.1):
![]() ,
(3.8)
,
(3.8)
где Jxy центробежный момент инерции сечения.
Если полярный момент инерции вычисляется
относительно начала системы координат
(рис. 3.1), то
![]() и
и
![]() ,
,
следовательно
![]() , (3.9)
, (3.9)
т .е.
сумма осевых моментов инерции сечения
относительно любых двух взаимно
перпендикулярных осей, проходящих
через данную точку равна полярному
моменту инерции этого сечения относительно
этой точки.
.е.
сумма осевых моментов инерции сечения
относительно любых двух взаимно
перпендикулярных осей, проходящих
через данную точку равна полярному
моменту инерции этого сечения относительно
этой точки.
Размерность моментов инерции L4. Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным, равным нулю.
Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю. Действительно, для симметричной фигуры всегда можно выделить два элемента ее площади (рис. 3.4), которые имеют одинаковые ординаты у1 = у2 = у и равные по величине, но противоположные по знаку абсциссы х1 = х и х2 = х. Тогда
![]() .
.
3.3 Зависимость между моментами инерции относительно параллельных осей
Пусть хс, ус
центральные оси
сечений,
![]() моменты инерции
сечения относительно этих осей. Определим
моменты инерции сечения относительно
новых осей х1, у1,
параллельных центральным осям и
смещенных относительно них на расстояния
а и d. Пусть dF
элементарная
площадка в окрестности точки М с
координатами х и у в центральной
системе координат. Из рис. 3.5 видно, что
координаты точки в новой системе
координат будут р
моменты инерции
сечения относительно этих осей. Определим
моменты инерции сечения относительно
новых осей х1, у1,
параллельных центральным осям и
смещенных относительно них на расстояния
а и d. Пусть dF
элементарная
площадка в окрестности точки М с
координатами х и у в центральной
системе координат. Из рис. 3.5 видно, что
координаты точки в новой системе
координат будут р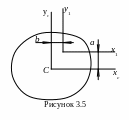 авны:
авны:
![]() .
.
Определим момент инерции сечения относительно оси х1:
![]() .
.
Очевидно, что первый интеграл дает
![]() ,
второй
,
второй
![]() ,
т.к. исходная система координат
центральная, а третий
площадь сечения F.
Таким образом,
,
т.к. исходная система координат
центральная, а третий
площадь сечения F.
Таким образом,
![]() .
(3.10)
.
(3.10)
Аналогично,
![]() ,
(3.11)
,
(3.11)
![]() .
(3.12)
.
(3.12)
3.4 Моменты инерции простых сечений
3.4.1 Прямоугольник
О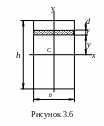 пределим
момент инерции сечения относительно
оси х0, проходящей через центр
тяжести прямоугольника высотой h
и шириной b параллельно
основанию (рис. 3.6). Выделим из прямоугольника
линиями, параллельными оси х
элементарную полоску высотой dу
и шириной b. Площадь
этой полоски dF = bdy,
расстояние от полоски до оси х равно
у. Подставим эти величины в выражение
момента инерции относительно оси х
(3.6):
пределим
момент инерции сечения относительно
оси х0, проходящей через центр
тяжести прямоугольника высотой h
и шириной b параллельно
основанию (рис. 3.6). Выделим из прямоугольника
линиями, параллельными оси х
элементарную полоску высотой dу
и шириной b. Площадь
этой полоски dF = bdy,
расстояние от полоски до оси х равно
у. Подставим эти величины в выражение
момента инерции относительно оси х
(3.6):
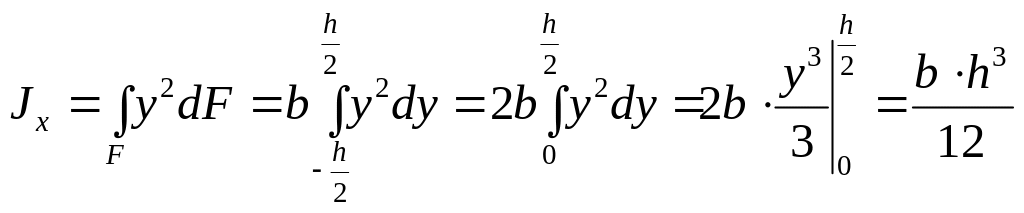 .
(3.13)
.
(3.13)
Аналогично, получим:
![]() . (3.14)
. (3.14)
Очевидно, что
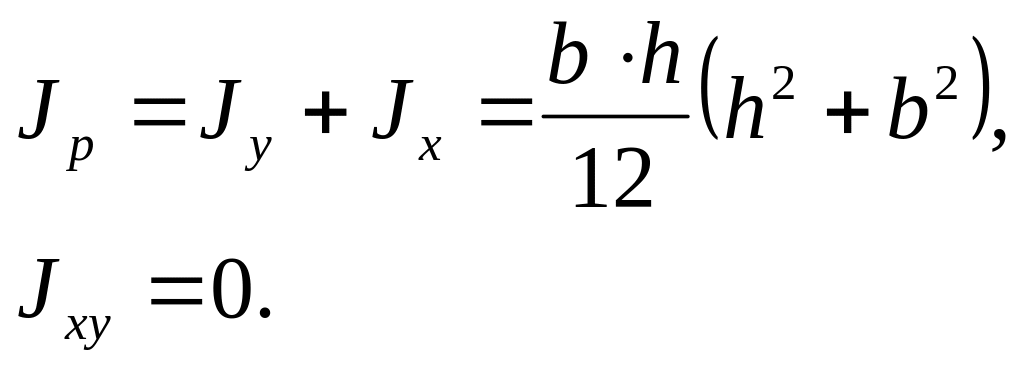
3.4.2 Треугольник
Определим момент инерции треугольника относительно оси х1, проходящей через основание:
![]()
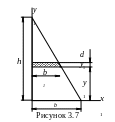 .
.
Элементарная площадка
![]() .
.
И
![]() ,
,
где b – основание треугольника, h – его высота.
Таким образом
![]() .
.
Расстояние от основания треугольника до центра тяжести равно:
![]() .
.
По формуле переноса находим момент инерции относительно центральной оси х, параллельно основанию:
![]() .
.
