2.7 Деформации при растяжении (сжатии)

П

Рисунок 2.11

ри растяжении стержня постоянного поперечного сечения длина увеличивается, а поперечные размеры уменьшаются (рис. 2.11).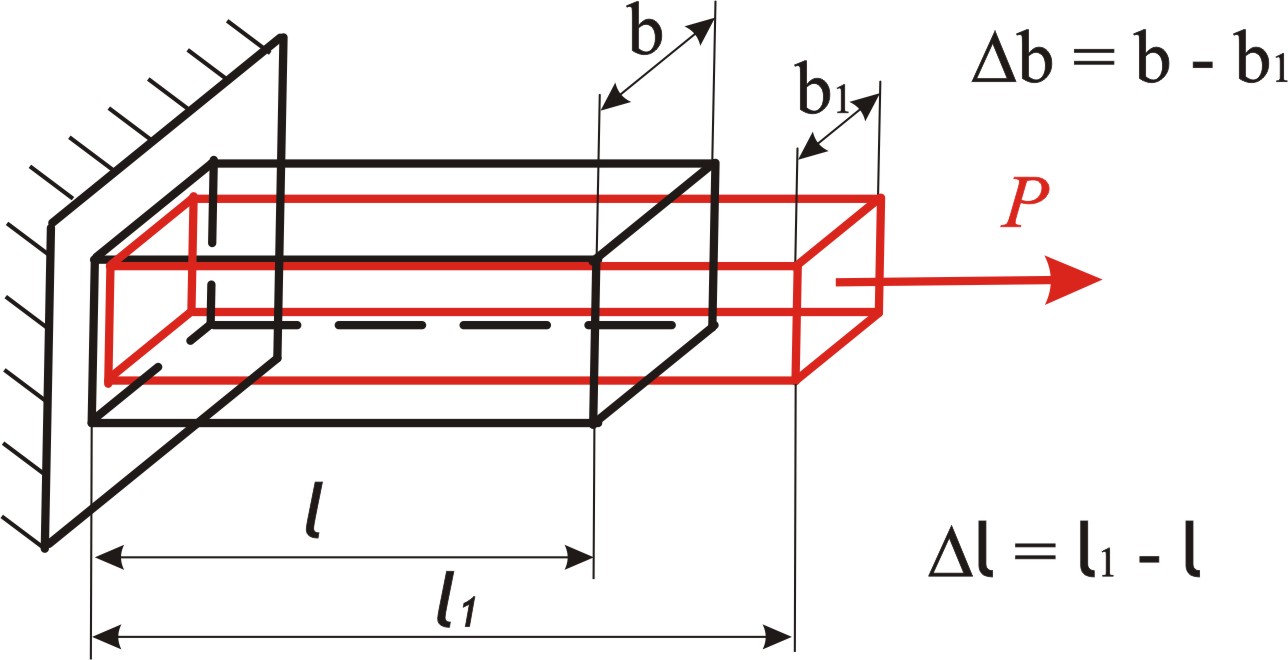

Из закона Гука:

. (2.4)

Учитывая то, что  = l / l и  = N / F имеем:

. (2.5)

Знаменатель EF называют жесткостью при растяжении  сжатии или продольной жесткостью.

Если мы возьмем произвольный поперечный размер b, то его изменение, отнесенное к его первоначальному значению, даст нам относительную поперечную деформацию (рис. 2.8):

. (2.6)

Между поперечной и продольной относительной деформацией при простом растяжении (сжатии) в пределах применимости закона Гука существует постоянное отношение. Абсолютная величина этого отношения носит название коэффициента Пуассона и обозначается буквой :

. (2.7)

Учитывая, что продольная и поперечная деформация всегда имеют противоположные знаки, получаем:

. (2.8)

Коэффициент Пуассона наряду с модулем продольной упругости характеризует упругие свойства материалов.

Значения  для различных материалов определяются экспериментально и изменяются в пределах 0    0,5 ( = 0 у пробки;  = 0,5 у резины;  = 0,3 у стали).

В некоторых случаях для обеспечения нормальной работы конструкций размеры их элементов нужно выбирать так, чтобы обеспечивалось условие жесткости. При растяжении (сжатии) условие жесткости имеет следующий вид:

, (2.9)

где l  изменение размеров детали; [l]  допускаемая величина этого изменения.

Расчет по условию жесткости всегда следует дополнять расчетом на прочность.

На растяжение работает и круглая труба, нагруженная внутренним давлением (рис. 2.12,а). Для определения напряжения в стенке такой трубы найдем из рассмотрения равновесия половины трубы (рис. 2.12,б) силу N, разрывающую стенку:

,

откуда

,

где р  давление в трубе; R_ср – средний радиус трубы; l  длина трубы.

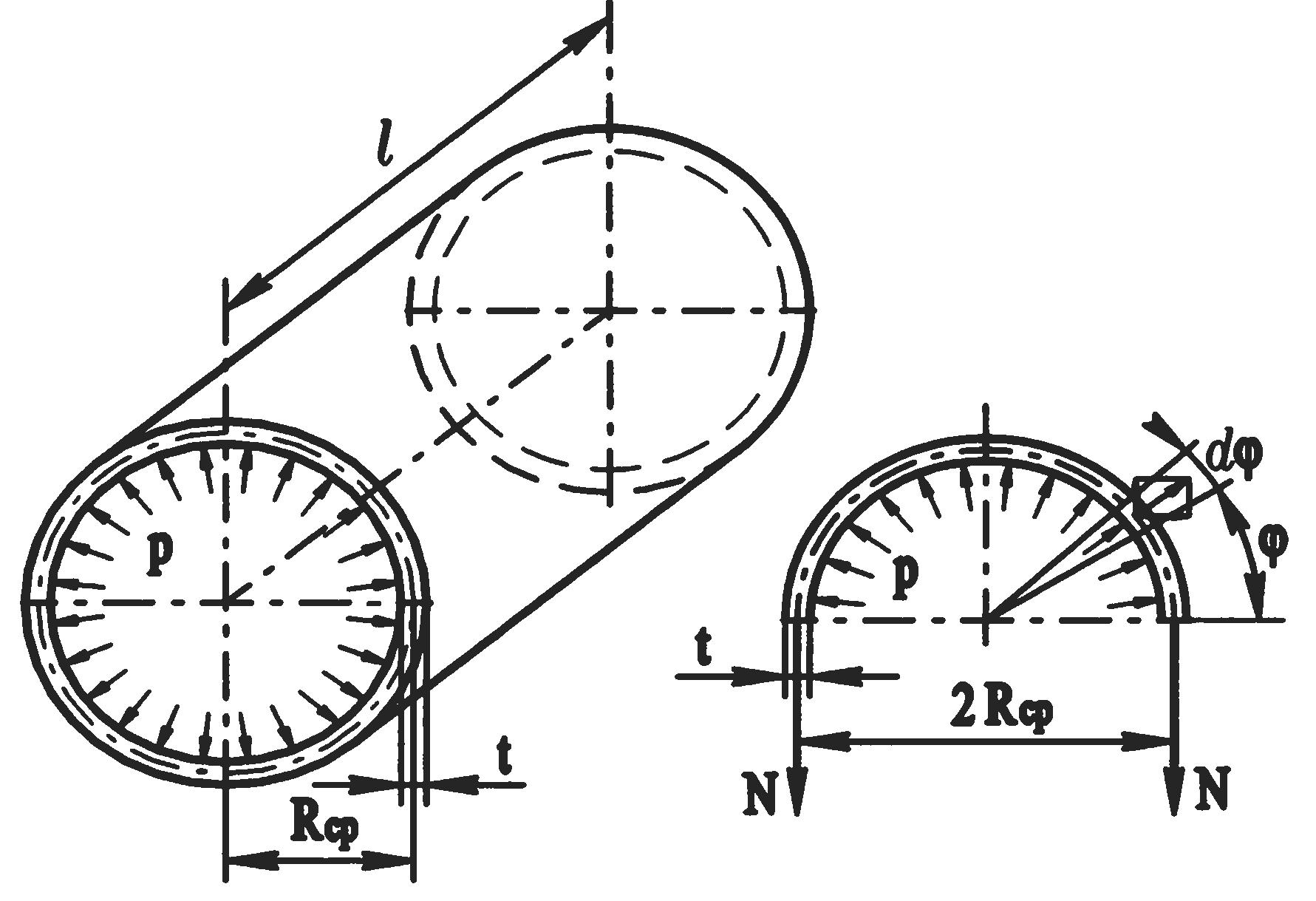
а) б)

Рисунок 2.12

Условие прочности трубы получаем в виде:

. (2.10)

где t  толщина стенки трубы.

Деформацию трубы  увеличение ее диаметра D  найдем из закона Гука : так как напряжение , а относительная деформация , то

откуда

. (2.11)

Вопросы для самопроверки

1. С какой целью проводятся механические испытания материалов? Какие напряжения являются опасными для пластичных и хрупких материалов?

2. Что такое механические характеристики материала?

3. Нарисуйте диаграмму растяжения Ст3 и укажите основные характеристики: предел пропорциональности, упругости, текучести, прочности.

4. Нарисуйте диаграмму растяжения хрупкого материала, укажите основные её особенности.

5. Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?

6. Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?

7. Что называется жесткостью поперечного сечения стержня при растяжении (сжатии)?

8. Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.

9. Что происходит с поперечными размерами стержня при его растяжении (сжатии)?

10. Что такое коэффициент Пуассона? В каких пределах он изменяется?

11. Что называется допускаемым напряжением? Как оно выбирается для пластичных и хрупких материалов?

12. Что такое твердость материала?

13. Назовите основные методы измерения твердости.