Частина і Основні поняття теорії ймовірностей. Тема класифікація подій. Операції над подіями.

1. Монету підкидають двічі. Визначити елементарні події цього експерименту.

2. Монету підкидають тричі. Визначити елементарні події цього експерименту.

3. Задано дві множини цілих чисел ω = {1, 2, 3} , Ω₂ = {1, 2, 3, 4}. Із кожної множини навмання беруть по одному числу. Визначити елементарні події цього експерименту - появу пари чисел.

4. Задано множину чисел Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Навмання із цієї множини беруть одне число. Побудувати такі випадкові події: 1) з'явиться число, кратне 2; 2) число кратне 3; 3) число, кратне 5.

5. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8,9,10,11,12,13,14, 15). Навмання з неї беруть одне число. Побудувати випадкові -події: 1) А – узяте число кратне 2; 2) В – кратне 3. Визначити.

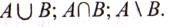
2. Описати простір елементарних подій, якщо випробування полягає в тому, що монету кидають двічі

3. Проводиться випробування кидання двох монет. Розглядаються такі події:

А – «випав герб на першій монеті»;

В – «випала цифра на першій монеті»;

С – «випав герб на другій монеті»;

D – «випала цифра на другій монеті».

Що означають події: а) А + С; б) В + D; в) А + D; г) В + С.

4. Вкажіть події, протилежні до подій:

А – «випали два герба при киданні двох монет»;

В – «вийнято білу кульку при витягуванні однієї кульки з урни, в якій 2 білих, 3 чорних і 4 червоних кульки»;

С – «три влучення при трьох пострілах»;

D – «хоча б одне влучення при п'яти пострілах»;

Е – «не більше двох попадань при п'яти пострілах»;

F – «виграш одного гравця при грі в шахи».

5. По мішені проводиться два постріли. Розглядаються події:

А – «влучення при першому пострілі»;

В – «влучення при другому пострілі».

Що означають події: а) б) в) г)

6. Чи утворюють повну групу наступні групи подій:

1. Експеримент – підкидання монети; події: А₁ - поява герба, А₂- поява цифри.

2. Експеримент – підкидання двох монет; події: А₁ - поява двох герба, А₂- поява двох цифри.

3. Експеримент –два вистріли по мішені; події: А₁ - жодного влучення, А₂- одне влучення, А₃- два влучення.

4. Експеримент –два вистріли по мішені; події: А₁ - хоч би одне влучення, А₂- хоч би один промах.

5. Експеримент –виймання карти із колоди; події: А₁ - поява карти чирвової масті, А₂- поява карти бубнової масті, А₃ - поява карти трефової масті.

7. Чи є несумісними наступні події:

1. Експеримент – підкидання монети; події: А₁ - поява герба, А₂- поява цифри.

2. Експеримент – підкидання двох монет; події: А₁ - поява герба на першій монеті, А₂- поява цифри на другій монеті.

3. Експеримент –два вистріли по мішені; події: А₁ - жодного влучення, А₂ - одне влучення, А₃- два влучення.

4. Експеримент –два вистріли по мішені; події: А₁ - хоч би одне влучення, А₂- хоч би один промах.

5. Експеримент –виймання карти із колоди; події: А₁ - поява двох чорних карт, А₂- поява туза, А₃ - поява дами.

8. Стрілець тричі стріляє в ціль. Нехай подія Аі полягає у влученні в ціль у результаті і-го пострілу (і = 1, 2, 3). Що означає подія:

D = a₁ •A₂ •A₃;

B = a₁ + А₂ + А₃.

Виразіть через події a₁, А₂ та А₃ такі події:

F -- «влучення мало місце лише в результаті першого пострілу»;

G – «влучення мало місце в результаті кожного з трьох пострілів »;

Н - «влучення мало місце лише в результаті одного пострілу»;

Е – «влучення мало місце не менше двох разів»;

К – «влучення мало місце не більше одного разу».

9. Систему складено з чотирьох блоків, кожний з яких працює або відказує незалежно від інших. Події A_i={ i-й блок відказав, i= 1; 2; 3,4}. Виразити через події А_і та протилежні їм такі події: В={відказав тільки один блок}, С={відказав принаймні один блок},

D={відказали три блоки}, Е={жодний блок не відказав}.

10. На модульній контрольній роботі студентам запропоновано 9 задач: 4 – першого рівня складності, 3 – другого і дві – третього рівня. Події

А_і={розв'язання i-ї задачі першого рівня, і=1,2,3,4}, B_j={розв'язання j-ї задачі другого рівня, j = 1,2,3}.

C_k={розв'язання k-ї задачі третього рівня, k =1, 2}, D={одержання позитивної оцінки}.

Виразити подію D через події А_і, B_j, C_k, якщо для одержання позитивної оцінки необхідно розв'язати всі задачі першого рівня, принаймні дві другого рівня і принаймні одну третього рівня.