Задача* 51.

Правила диференціювання.

1. Земельна ділянка мас форму рівностороннього трикут­ника з висотою x. Знайдіть S¢(3 ), якщо S(x) - площа цієї ділянки.

2. Дано рівнобічну трапецію з основами x і 3х, бічною стороною 2х. Знайдіть S¢( ), якщо S(x) - площа цієї трапеції.

3. Маса m неоднорідного стержня розподіляється за законом m=l²+3l+5, де l- довжина стержня. Знайдіть: а) середню лінійну густину стержня завдовжки 5 см; б) лінійну густину стержня при l=10 см.

4. Кількість електрики в провіднику змінюється за зако­ном Q=(2t²–4t) Кл. Знайдіть середнє значення сили струму за перші дві секунди і силу струму в кожну другу і п'яту секунди.

5. Дві матеріальні точки рухаються прямолінійно за законами s₁(t)=2,5t²–6t+1, s₁(t)=0,5 t²+2t-3, де t- час у секундах, s- шлях у метрах. В який момент часу швидкості їх однакові?

6. Дві матеріальні точки рухаються прямолінійно за зако­нами s₁(t)=t²–6t–2, s₁(t)=4t+5, де t - час у секундах, s - шлях у метрах. В який момент часу швидкість першої точки вдвічі більша за швидкість другої?

7. Снаряд, випущений вертикально зенітною батареєю з початковою швидкістю v₀ рухається за законом k= v₀t–g t²/2. Який шлях пройде снаряд від t= 0 до моменту, коли швидкість дорівнюватиме 5 м/с?

8. Точка рухається за законом s(t)=5t-t². Який шлях пройде точка за час від t= 0 до моменту, коли швидкість дорівнюватиме нулю?

9. Число 36 подайте у вигляді суми двох невід'ємних до­данків так, щоб сума квадратів цих чисел була найменшою.

10. Число 6 подайте у вигляді суми двох невід'ємних до­данків так, щоб добуток цих чисел був найбільшим.

11. Знайдіть швидкість гармонічного коливального руху заряджених частинок, якщо s=Asin(ωt+φ). За якого значення часу ця швидкість дорівнюватиме нулю?

12. Тіло кинуто з початковою швидкістю v₀ під кутом α до горизонту. Знайдіть положення і миттєву швидкість тіла в будь-який момент часу.

13. Балістична ракета від моменту запуску рухається зі швидкістю v(t)= 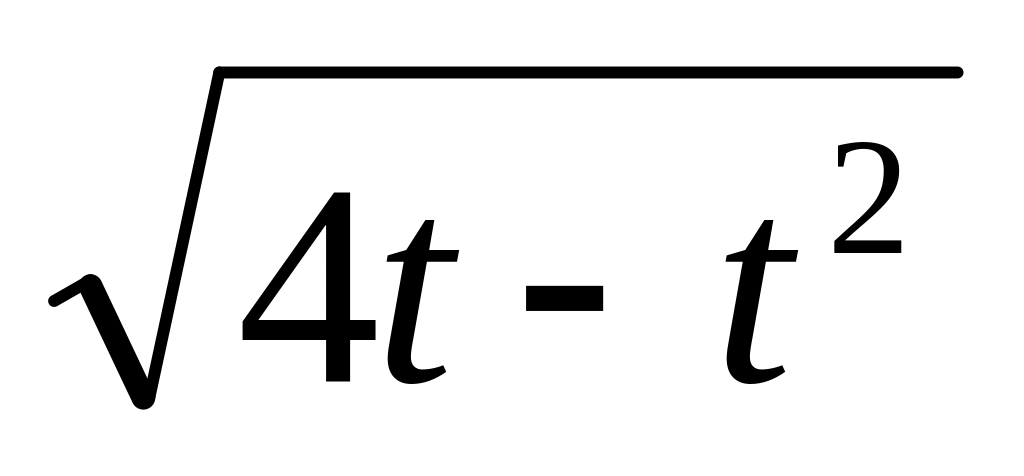(км/с). Знайдіть швидкість ракети в той момент, коли її прискорення дорівнює нулю.

14. Кинутий на стіл тенісний м'ячик підстрибує так, що висота його над поверхнею стола змінюється (в сантиметрах) за законом k(t)=5(1+sin(5t+^π/₂))/(t+1) (t в секундах). Яку швидкість і прискорення матиме м'ячик у момент часу: а) t =^π/₂; б) t = 2?

15. Заряд q змінюється в провіднику з часом за законом q=2sin³ 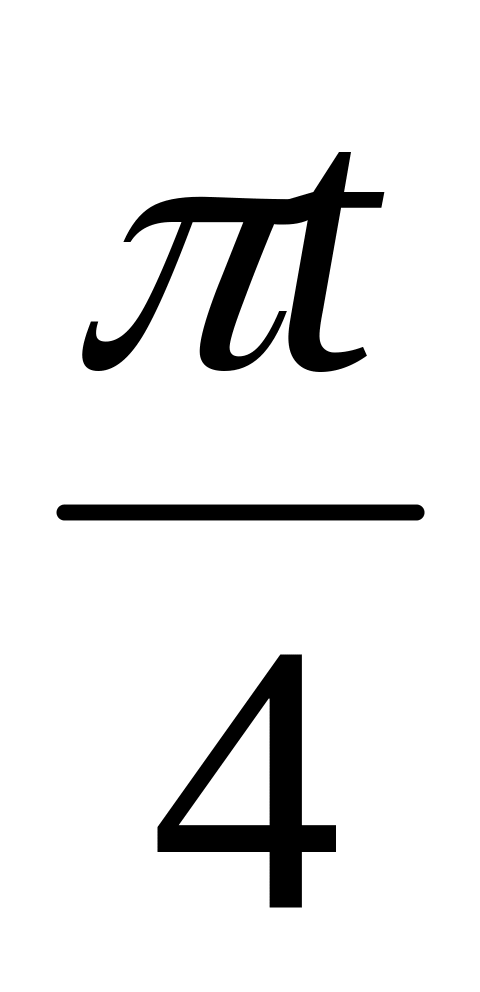+tcos² . Знайдіть силу струму провідника в момент часу t=2 с.

16. Знайдіть швидкість крильчатки електричного двигуна під час короткого замикання у момент ввімкнення, якщо рух задається функцією x(t)=2sin^t/₁₁+3tgt- .

17. Заряд конденсатора в електричному колі описується формулою q=2sin 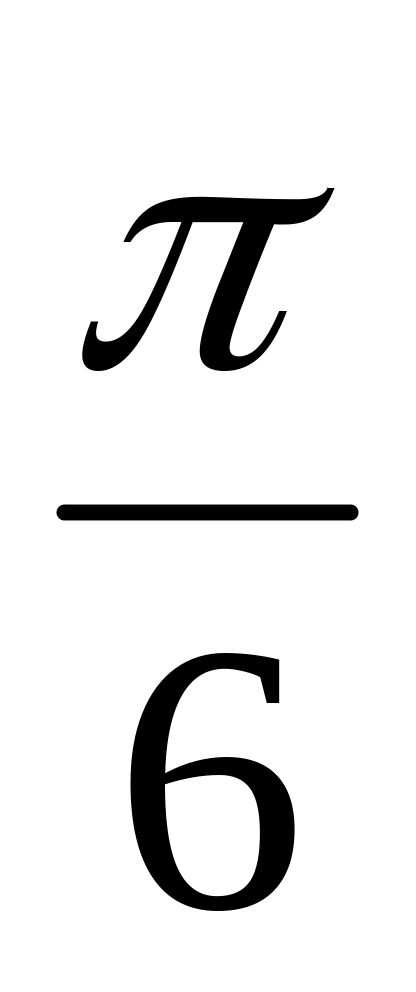cos3t+2sin4tcos . Знайдіть силу струму.

18. Відстань від підлоги до нижнього краю картини, яка висить на стіні, дорівнює а(м), а до її верхнього краю - b (м). Під яким кутом зору бачить картину людина, зріст якої с(см) і яка перебуває на відстані х (м) від стіни, де висить картина? Розгляньте випадок а > с і знайдіть відстань х, для якої кут зору буде найбільшим.

19. Картина заввишки 1,4 м висить на стіні так, що її нижній край на 1,8 м розміщений вище від ока спостерігача. На якій відстані від стіни має знаходитись спостерігач, щоб кут тару його був максимальним?

20. Залежність шляху від часу експериментальне заряджених частинок визначається за формулою s(t)=(t+ 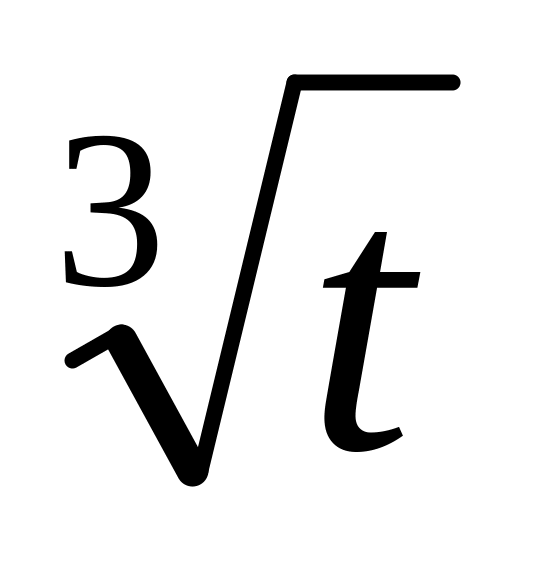)(1/t+1/ ). Знайдіть середню швидкість руху цих частинок для проміжку часу t= [2;3].

21. Закон зміни температури Т тіла залежно від часу t задається рівнянням T= 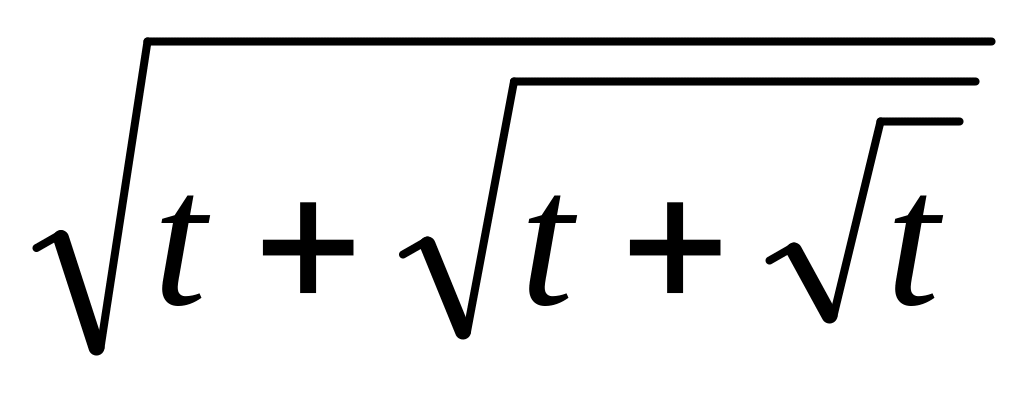. 3 якою швидкістю змінюється температура тіла в момент часу t = 4 с?

22. Периметр рівнобедреного трикутника дорівнює 2р. Якими мають бути його сторони, щоб об'єм конуса, утвореного обертанням цього трикутника навколо своєї висоти, був найбільшим?

23. Знайдіть найменшу довжину стріли крана, необхідну для монтажу плит перекриття споруди заввишки Н = 12,50 м, завширшки Q = 10,00 м, за умови, що кран може рухатися вздовж фасаду споруди паралельно йому, якщо висота основи стріли крана над землею k₁= 1,50 м, відстань між стрілою і стіною споруди має бути не менше m=1,00 м.

24. Шлях, пройдений ліфтом, визначається рівнянням s(t)=(t+1)/(t²+3). Знайдіть швидкість і прискорення в будь-який момент часу t (s-шлях у метрах, t- час у секундах).

25. Колесо обертається так, що залежність кута повороту радіуса колеса від часу задається рівнянням φ(t)=1+(t-1)/(t²+1). Знайдіть кутову швидкість і кутове прискорення в будь-який момент часу t.

26. Посудина у формі півкулі радіуса R(см) наповнюється водою зі сталою швидкістю Q (л/с). Визначте швидкість підвищення рівня води на висоті h (см) і покажіть, що вона обер­нено пропорційна площі вільної поверхні води.

27. Дано функції f(x)=х²–х і g(x)=х²+х. За яких зна­чень х функція f(x) зростає вдвічі швидше, ніж функція g(x)? Чи існує таке значення х, за якого функції змінюються з однаковою швидкістю?

28. З конусоподібної лійки висипається пісок зі сталою швидкістю Q (м³/с). З якою швидкістю змінюватиметься рівень піску в лійці?

29. Матеріальна точка рухається по прямій за законом s(t)=t³–2t+5, де s(t) - шлях у метрах; t - час у секундах. У який момент часу з проміжку [0;4] швидкість руху точки найбільша? Знайдіть цю швидкість.

30. Матеріальна точка здійснює затухаючі гармонійні коливання, які описуються рівнянням x(t)=4(t+cos(6t+^π/₂))/(t+1), де x(t)- зміщення точки від початкового положення. Які швидкість і прискорення матиме точка в моменти часу: а) t=^π/₂ c; б) t=^π/₄ c?

31. Для силосу треба приготувати довгу яму з поперечним перерізом у формі рівнобічної трапеції, бічні сторони і менша основа якої мають довжини по 10м. Яким має бути гострий кут х трапеції, щоб площа її поперечного перерізу була найбільшою?