3.3 Виды модуляции сигналов

3.3.1 Частотно-импульсная модуляция

Для формирования последовательностей прямоугольных импульсов с переменным значением частоты их следования достаточно часто используется метод частотно-импульсной модуляции (ЧИМ). При этом виде модуляции в соответствии с модулирующей функцией Х(t) изменяется частота f следования импульсов.

Если при ЧИМ неизменной остается длительность 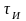импульсов, то такую модуляцию называют частотно-импульсной модуляцией первого рода и обозначают как ЧИМ1 (рис. 3.1,а,б).

Если при ЧИМ неизменной остается скважность Q (отношение периода следования импульсов к их длительности), то такую модуляцию называют частотно-импульсной модуляцией второго рода – ЧИМ2 (рис. 3.1,а,в).

В качестве примера на рис. 3.1,в приведены временные диаграммы для 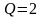. В общем случае скважность может иметь любые значения в диапазоне от 1 до .

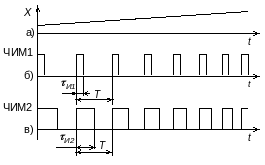
Рисунок 3.1 – Временные диаграммы при частотно-импульсной модуляции

Если связь между модулирующий функцией и частотой следования импульсов на выходе модулятора определяется линейной зависимостью, то передаточная характеристика модулятора будет иметь вид

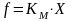, (3.1)

где К_М – коэффициент передачи модулятора, который может быть определен как

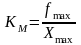, (3.2)

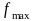– максимальное значение частоты следования импульсов на выходе модулятора;

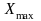– максимальное значение модулирующей функции.

В случае линейной передаточной характеристики (см. выражение (3.1)) остальные параметры импульсной последовательности, полученной в результате ЧИМ1 и ЧИМ2 могут быть определены выражениями, которые приведенны в табл. 3.1.

Коэффициент 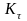в табл. 3.1 определяет соотношение между длительностью выходных импульсов и минимальным значением периода 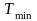их следования при ЧИМ1 (коэффициент 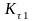) или текущим значением периода 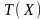их следования при ЧИМ2 (коэффициент ).

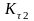Таблица 3.1 – Выражения для определения параметров импульсных последовательностей

Параметр	ЧИМ1	ЧИМ2
Т
Q
k

В тех случаях, когда параметры импульсной последовательности целесообразно представить в относительных единицах, следует воспользоваться выражениями, приведенными в табл. 3.2.

Таблица 3.2 – Выражения для определения относительных значений параметров импульсных последовательностей

Параметр	ЧИМ1	ЧИМ2
	0,05
	– 0,05
Q		2
k		0,5

Во всех случаях относительные единицы определялись как

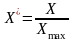; (3.3)

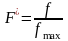; (3.4)

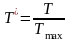; (3.5)

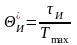; (3.6)

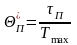, (3.7)

а кроме того, задавались следующими условиями

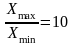; (3.8)

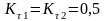. (3.9)

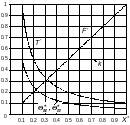
Все зависимости по табл. 3.2 (кроме скважности) представлены в графическом виде на рис. 3.2,а для ЧИМ1 и на рис. 3.2,б для ЧИМ2.

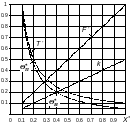
а) б)

Рисунок 3.2 – Зависимости относительных значений параметров импульсных последовательностей от модулирующей функции при ЧИМ1 (а) и при ЧИМ2 (б)

Суть процессов в частотно-импульсном модуляторе поясняет рис. 4.11. Входное напряжение 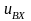с некоторым коэффициентом пропорциональности K преобразуется в ток

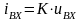. (3.10)

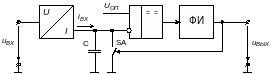
а)

б)

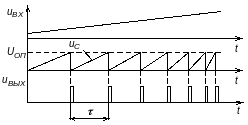
Рисунок 3.3 – Схема (а) и временные диаграммы напряжений (б) частотно-импульсного модулятора

В исходном состоянии ключ SA разомкнут и конденсатор С, предварительно разряженный до нуля, начинает заряжаться со скоростью

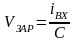. (3.11)

Напряжение на конденсаторе достигает значения опорного напряжения 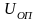, по истечении временного интервала 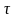, который может быть определен как

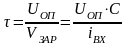. (3.12)

При выполнении условия 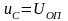компаратор переключается в другое устойчивое состояние, что приводит к срабатыванию формирователя импульсов (ФИ). Последний формирует короткий импульс, который является выходным сигналом модулятора. По фронту этого сигнала замыкается ключ SA и конденсатор С начинает быстро разряжаться до нуля. Компаратор при этом возвращается в свое исходное состояние. Далее процессы полностью повторяются.

Очевидно, что временной интервал является периодом следования выходных импульсов (длительностью временного интервала разряда конденсатора С пренебрегаем). Частота выходных импульсов при этом может быть определена как

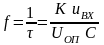, (3.13)

из последнего выражения видно, что чем больше значение входного напряжения, тем выше частота выходного сигнала.